Feynmann - Feynmann 8

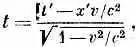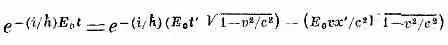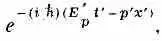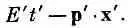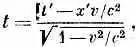
и теперь наша амплитуда меняется так:

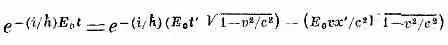
В штрихованной системе она меняется в пространстве и во времени. Если амплитуду записать в виде

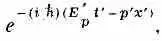
то видно, что Е ' р = Е 0 / Ц ( 1 - v 2/с 2). Это энергия, вычисленная по классическим правилам для частицы с энергией покоя Е 0 , движущейся со скоростью v ; p '= E ' p v / c 2 — соответствующий импульс частицы.

Вы знаете, что х m = ( t , х, y , z) и р m = (Е, р х , р y , р г ) — четырехвекторы, a p m x m = Et - р · х—скалярный инвариант. В системе покоя частицы p m x m просто равно Et ; значит, при преобразовании в другую систему Et следует заменить на

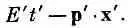
Итак, амплитуда вероятности для частицы, импульс которой есть р, будет пропорциональна

где Е р — энергия частицы с импульсом р, т. е.

а Е 0 , как и прежде, —энергия покоя. В нерелятивистских задачах можно писать

где W p — избыток (или нехватка) энергии по сравнению с энергией покоя М sс 2частей атома. В общем случае в W p должны были бы войти и кинетическая энергия атома, и его энергия связи или возбуждения, которые можно назвать «внутренней» энергией. Тогда мы бы писали

а амплитуды имели бы вид

Мы собираемся все расчеты вести нерелятивистски, так что именно таким видом амплитуд вероятностей мы и будем поль­зоваться.

Заметьте, что наше релятивистское преобразование снаб­дило нас формулой для изменения амплитуды атома, движу­щегося в пространстве, не требуя каких-либо добавочных до­пущений. Волновое число ее изменений в пространстве, как это следует из (5.9), равно

а, значит, длина волны

Это та самая длина волны, которую мы раньше использовали для частиц с импульсом р. Именно таким путем де-Бройль впервые пришел к этой формуле. Для движущейся частицы частота изменения амплитуды по-прежнему дается формулой

Абсолютная величина (5.9) равна просто единице, так что для частицы, движущейся с определенной энергией, вероят­ность обнаружить ее где бы то ни было - одна и та же повсю­ду и со временем не меняется. (Важно отметить, что амплиту­да это комплексная волна. Если бы мы пользовались веще­ственной синусоидой, то ее квадрат от точки к точке менялся бы, что было бы неверно.)

Конечно, мы знаем, что бывают случаи, когда частицы дви­жутся от одного места к другому, так что вероятность зависит от положения и изменяется со временем. Как же нужно опи­сывать такие случаи? Это можно сделать, рассматривая ампли­туды, являющиеся суперпозицией двух или большего числа амплитуд для состояний с определенной энергией. Такое поло­жение мы уже обсуждали в гл. 48 (вып. 4), причем именно для амплитуд вероятности! Мы нашли тогда, что сумма двух ам­плитуд с разными волновыми числами k (т. е. импульсами) и частотами w (т. е. энергиями) приводит к интерференционным буграм, или биениям, так что квадрат амплитуды меняется и в пространстве, и во времени. Мы нашли также, что эти биения движутся с так называемой «групповой скоростью», опреде­ляемой формулой