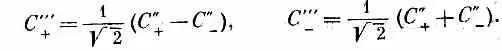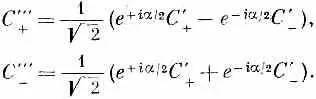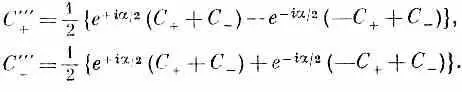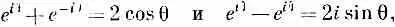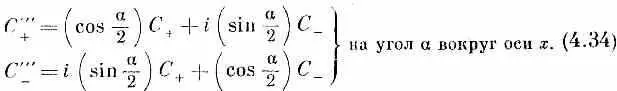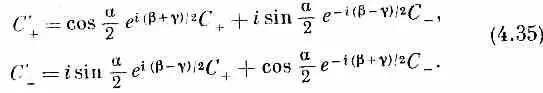Feynmann - Feynmann 8

Последний поворот на -90° вокруг оси у" переводит нас в систему х'", у'", z '"; из (4.33) следует

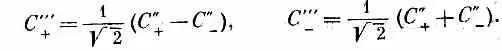
Сочетая эти два последних преобразования, получаем

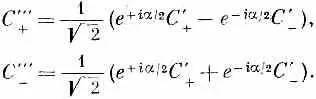
Подставляя сюда вместо С' + и С' -(4.32), придем к полному преобразованию

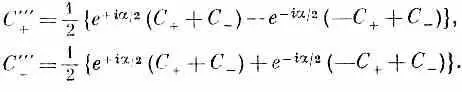
А если вспомнить, что

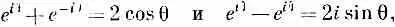
то эти формулы можно записать проще:

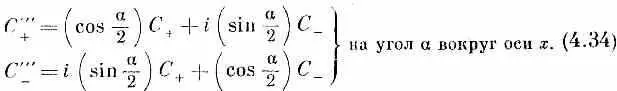
Это и есть наше искомое преобразование для поворота вокруг оси х на любой угол a. Оно лишь чуть посложнее остальных,

§ 6. Произвольные повороты

Теперь уже понятно, как быть с произвольным поворотом. Во-первых, заметьте, что любая относительная ориентация двух систем координат может быть описана тремя углами (фиг. 4.9).

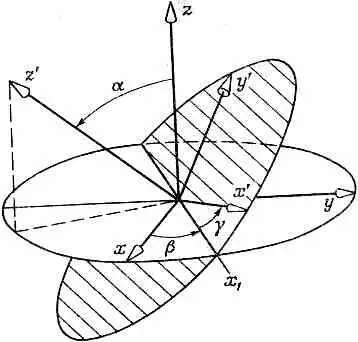
Фиг. 4.9. Ориентацию лю­бой системы координат х' , у', г' по отношению к другой системе х, у, z можно опре­делить с помощью углов Эйлера a , b , g .

Если есть система осей х', у', z ' , ориентированных относительно х, у, z как угодно, то соотношение между ними можно описать тремя углами Эйлера a, b и g, определяющими три последовательных поворота, которые переводят систему х, у, z в систему х', у', z ' . Отправляясь от x, у, z, мы повора­чиваем нашу систему на угол bets вокруг оси z, перенося ось х на линию х'. Затем мы проводим поворот на угол а вокруг этой временной оси х 1 , чтобы довести ось z до z '. Наконец, по­ворот вокруг новой оси z (т. е. вокруг z ' ) на угол g переведет ось х 1 в х', а ось у в у'. Мы знаем преобразования для каж­дого из трех поворотов — они даются формулами (4.19) и (4.34). Комбинируя их в нужном порядке, получаем

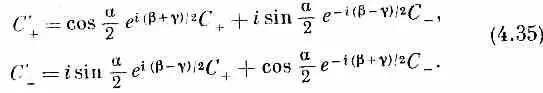
Итак, начав просто с некоторых предположений о свойст­вах пространства, мы вывели преобразование амплитуды при любом повороте. Это означает, что если нам известны ампли­туды того, что любое состояние частицы со спином 1/ 2перейдет в один из двух пучков прибора Штерна — Герлаха S с осями х, у, z , то мы можем подсчитать, какая часть перейдет в каж­дый пучок в приборе Т с осями х', у' и z'. Иначе говоря, если имеется состояние y частицы со спином 1/ 2, у которого ам­плитуды пребывания вверху и внизу по отношению к оси z системы координат х, у, z равны С +=<+|y> и С -=<-|y>, то тем самым мы знаем амплитуды С + и C -пребывания вверху и внизу по отношению к оси z ' любой другой системы х', у", z ' , Четверка коэффициентов в (4.35) — это члены «матрицы преобразования», с помощью которой можно проецировать амплитуды частицы со спином 1/ 2в другие системы ко­ординат.

Теперь решим несколько примеров, чтобы посмотреть, как все это работает. Возьмем следующий простой вопрос. Пустим атом со спином 1/ 2через прибор Штерна — Герлаха, пропу­скающий только состояние (+z). Какова амплитуда того, что атом окажется в состоянии (+ x )? Ось + х — это все равно, что ось +z' системы, повернутой на 90° вокруг оси у. Поэтому в этой задаче проще воспользоваться выражением (4.32), хотя, конечно, можно применить и полное уравнение (4.35). По­скольку С + =1 и С - =0, то получится С' + =1/Ц2. Вероятности -это квадраты модулей этих амплитуд; таким образом, 50% шансов за то, что частица пройдет сквозь прибор, отбирающий состояние ( +х ) . Если бы мы поинтересовались состоянием (- х ) , то амплитуда оказалась бы -1/Ц2, что опять дало бы вероятность 1/ 2, чего и следовало ожидать из симметрии про­странства. Итак, если частица находится в состоянии (+z), то ей в равной степени вероятно побывать в состояниях (+ x ) и (- х ) . Но фазы противоположны.