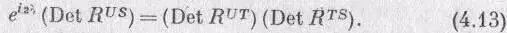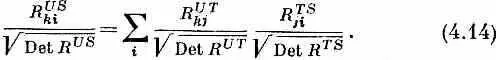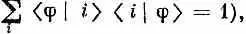Feynmann - Feynmann 8

Во-первых, следует напомнить, что (4.11) — это математи­ческое определение «произведения» двух матриц. (Просто очень удобно говорить « R US есть произведение R UT и R TS ».) Во-вторых, существует математическая теорема (которую для используемых здесь матриц 2X2 вы легко докажете), утверждающая, что детерминант «произведения» двух матриц есть произведение их детерминантов. Применив эту теорему к (4.12), получим

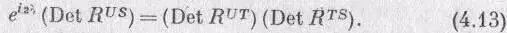
(Мы отбрасываем нижние индексы, они здесь ничего полезного нам не сообщают.) Да, слева стоит 2S! Вспомните, что мы имеем дело с матрицами 2x2; каждый член в матрице R US ki умножен на е i d , а каждый член в детерминанте (состоящий из двух мно­жителей) получается умножением на е i 2 d . Извлечем из (4.13) корень и разделим на него (4.12):

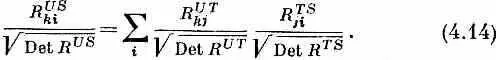
Добавочный фазовый множитель исчез.

Дальше оказывается, что если мы хотим, чтобы все наши амплитуды в любом заданном представлении были нормированы (а это, как вы помните, означает, что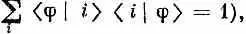

то у всех матриц поворота детерминанты окажутся чисто мни­мыми экспонентами, наподобие е i a . (Мы не будем этого дока­зывать; вы сами потом увидите, что это всегда так.) Значит, мы сможем, если захотим, выбрать все наши матрицы поворота R так, чтобы фаза их получалась однозначно, взяв Det R =1. Это будет делаться так. Пусть мы каким-то произвольным об­разом определили матрицу поворота R . Возьмем за правило «приводить» ее к «стандартной форме», определяя

Для получения однозначных фаз мы просто умножаем каждый член в R на один и тот же фазовый множитель. В дальнейшем мы будем всегда предполагать, что наши матрицы были приве­дены к «стандартной форме»; тогда мы сможем пользоваться прямо формулой (4.11) без каких-либо добавочных фазовых множителей.

§ 3. Повороты вокруг оси z

Теперь мы уже подготовлены к тому, чтобы отыскать матри­цу преобразования R ji , связывающую два разных представления, Владея нашим правилом объединения поворотов и нашим предположением, что в пространстве нет предпочтительного направ­ления, мы владеем ключом для отыскания матрицы любого произвольного поворота. Решение здесь только одно. Начнем с преобразования, которое отвечает повороту вокруг оси z . Пусть имеются два прибора S и Т, поставленных друг за дру­гом вдоль одной прямой; оси их параллельны и смотрят из страницы на вас (фиг. 4.4, а).

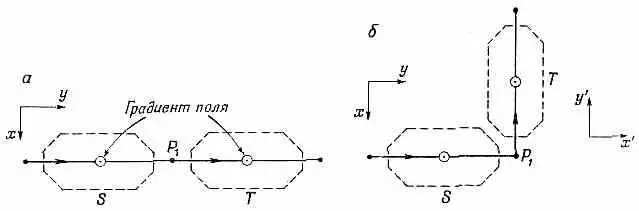
Фиг. 4.4. Поворот на 90° вокруг оси z .

Это их направление мы примем за ось z . Ясно, что если пучок в приборе S идет вверх (к + z ), то то же будет и в аппарате Т. Точно так же, если он в S идет вниз, то и в Т он направится вниз. Положим, однако, что прибор Т был повернут на какой-то угол, но его ось, как и прежде, параллельна оси прибора S , как на фиг. 4.4, б. Интуитивно хочется сказать, что пучок (+) в S будет по-прежнему пере­ходить в пучок (+) в Т, потому что и поля, и их градиенты характеризуются тем же физическим направлением. И это вполне правильно. Точно так же и пучок (-) в S будет перехо­дить в пучок (-) в Т. Тот же результат применим для любой ориентации Т в плоскости ху прибора S . Что же отсюда сле­дует для связи между С ' + = <+T|y>, С ' - =<- T |y> и С + =<+ S |y>, С - = <- S |y>? Можно подумать, что любой поворот вокруг оси z «системы отсчета» базисных со­стояний оставляет амплитуды С± пребывания «вверху» и «вни­зу» теми же, что и раньше, и написать С ' + =С + и С' -= С - . Но это неверно. Все, что можно отсюда заключить,— это, что при таких поворотах вероятности оказаться в «верхнем» пучке при­боров S и Т одинаковы, т. е.