Feynmann - Feynmann 8

§ 2 . Преобразование к повернутой системе координат

Рассмотрим опять «усовершенствованный» прибор Штерна— Герлаха, описанный в предыдущей главе. Пучок частиц со спи­ном 1/ 2, входящих слева, расщепляется, вообще говоря, на два пучка, как показано схематически на фиг. 4.1.

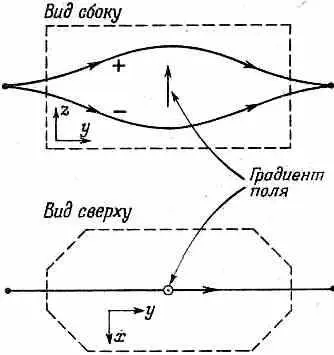
Фиг. 4.1. «Усовершенствованный» прибор Штерна — Герлаха с пучками частиц со спином 1/ 2.

(При спине 1 пучков было три.) Как и раньше, пучки в конце снова сводятся в одно место, если только один из них не будет перекрыт «перегородкой», которая перехватит его на полпути. На рисунке имеется стрелка, которая показывает направление роста величины поля, скажем положение магнитного полюса с острым наконечником. Эта стрелка пусть будет представлять собой на правление вверх для данного прибора. В каждом аппарате ее положение фиксировано, что позволяет указывать взаимную ориентацию нескольких приборов относительно друг друга. Наконец, предположим еще, что направление магнитного поля относительно стрелки во всех магнитах одинаково.

Будем говорить, что атомы из «верхнего» пучка находятся по отношению к этому прибору в состоянии (+), атомы из «нижнeгo» — в состоянии (-). (Нуль-состояния для спина 1/ 2не

существует.)

Положим теперь, что мы поставили два наших усовершен­ствованных прибора Штерна — Герлаха один за другим фиг. 4.2, а).

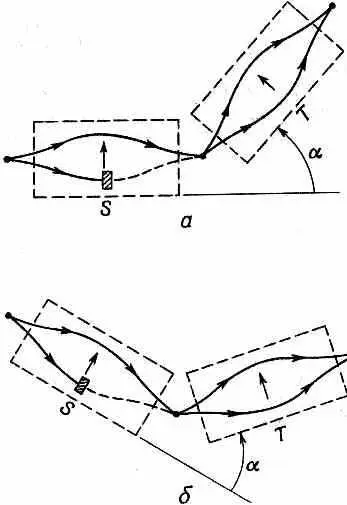
Фиг. 4.2. Два эквивалентных эксперимента.

Первый (назовем его S ) можно употребить на то, что­бы приготовлять чистое состояние (+ S ) или (- S ), загораживая то один, то другой пучок. [На рисунке приготовляется чистое состояние (+ S ).] При любом расположении всегда есть неко­торая амплитуда того, что частица, выходящая из S , окажется в пучке ( + Т) или (- Т) второго прибора. Всего таких ампли­туд четыре: амплитуды перехода от (+ S ) к (+ T ), от (+ S ) к ( - Т), от (- S ) к (+Т) и от (- S ) к (- T ). Эти амплитуды — просто четыре коэффициента матрицы преобразования R jiперехода от представления S к представлению Т. Можно счи­тать, что первый прибор «приготовляет» определенное состояние в одном представлении, а второй «анализирует» это состояние в терминах второго представления. Мы хотим научиться отве­чать на такие вопросы: если, загородив один из пучков в S , мы приготовили атом в данном состоянии, например в состоянии (+5), то каково будет изменение, которое он испытает, пройдя через прибор Т, который настроен на состояние (- T )? Резуль­тат, конечно, будет зависеть от углов между системами S и Т.

Мы должны объяснить, почему есть надежда найти коэф­фициенты R ji теоретически. Почти невозможно поверить, что если у частиц спин был выстроен в направлении +z, то есть хоть какой-то шанс обнаружить, что ее спин ориентирован в направлении + x или в каком-либо другом направлении. Это дей­ствительно почти невозможно. Но все же не совсем. Это на­столько невозможно, что остается лишь один путь, каким это происходит, а если этот путь один, то его уже можно найти.

Первое рассуждение можно провести так. Предположим, что, как показано на фиг. 4.2, а, прибор Т направлен вверх под уг­лом а относительно S . Пусть через S проходит только пучок (+), а через Т — только пучок (-). Мы измерили некоторую вероятность того, что частицы, выходя из S , пройдут сквозь Т. Теперь предположим, что мы делаем второе измерение при­бором, показанным на фиг. 4.2, б. Относительная ориентация S и Т одинакова, но вся система расположена в пространстве под другим углом. Мы хотим предположить, что оба опыта приведут к одному и тому же значению вероятности того, что частица в чистом состоянии относительно S окажется в некото­ром определенном состоянии относительно Т, Иными словами, мы предполагаем, что результат любого опыта такого рода оди­наков, что сама физика одинакова, как бы весь прибор ни был ориентирован в пространстве. (Вы скажете: «Это самоочевидно». Но это все же только предположение, и оно «правильно» только тогда, если так действительно бывает.) Это означает, что коэффициенты R ji зависят лишь от взаимного расположения S и Т в пространстве, а не от абсолютного их расположения. Выражаясь иначе, R ji зависит только от поворота, который переводит S в Т, потому что общим для фиг. 4.2, а и б, очевидно, является трехмерный поворот, переводящий прибор S в положе­ние прибора Т. Когда матрица преобразования R ji зави­сит, как в нашем случае, только от поворота, ее называют матрицей поворота.