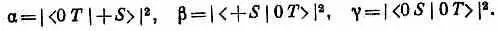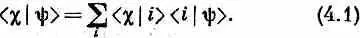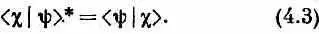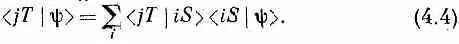Feynmann - Feynmann 8

* На языке наших прежних обозначений

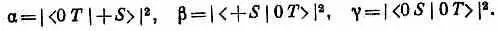
* Мы не собираемся вкладывать в слова «базисное состояние» что-либо сверх того, что здесь сказано. Не следует переводить «базис» как «основу» и хоть в каком-то смысле считать их «основными состояниями». Слово «базис» понимается как «система описания», скажем, в таком смыс­ле, как в выражении «число в десятичной системе».

* Произносить надо так: (+ S )—«плюс- S »; (0 S ) — «нуль - S »; ( - S ) — «минус- S ».

Глава 4

СПИН ОДНА ВТОРАЯ

§ 1. Преобразование амплитуд

§ 2. Преобразование к повернутой системе координат

§ 3. Повороты вокруг оси z

§ 4. Повороты на 180° и на 90 вокруг оси у

§ 5. Повороты вокруг оси x

§ б. Произвольные повороты

§ 1. Преобразование амплитуд

В предыдущей главе мы, пользуясь в ка­честве примера системой со спином 1, набросали общие принципы квантовой механики.

Любое состояние y можно описать через совокупность базисных состояний, задав амплитуды пребывания в каждом из них.

Амплитуда перехода из одного состоя­ния в другое может быть в общем слу­чае записана в виде суммы произведений амплитуд перехода в одно из базисных со­стояний на амплитуды перехода из этих базисных состояний в конечное положе­ние; в сумму непременно входят члены, относящиеся к каждому базисному состоя­нию;

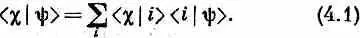
Базисные состояния ортогональны друг другу — амплитуда пребывания в одном, если вы находитесь в другом, есть нуль:

Амплитуда перехода из одного состоя­ния в другое комплексно сопряжена амп­литуде обратного перехода

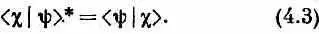
Мы немного поговорили о том, что базис для состояний может быть не один и что можно использовать (4.1), чтобы пе­рейти от одного базиса к другому. Пусть, например, мы знаем амплитуды < iS | y > обнаружения состояния y в лю­бом из базисных состояний i базисной системы S , но затем решаем, что лучше описывать состояние в терминах другой совокупности базисных состояний — скажем, состояний j , при­надлежащих к базису Т. Мы тогда можем подставить в общую формулу (4.1) jT вместо c и получить

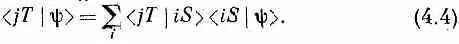
Амплитуды обнаружения состояния ( y ) в базисных состояниях ( j Т) связаны с амплитудами его обнаружения в базисных со­стояниях ( iS ) совокупностью коэффициентов < jT | iS > . Если базисных состояний N, то таких коэффициентов всего N 2 . Эту совокупность коэффициентов часто называют «матрицей преобразования от представления S к представлению Т». Математически это выглядит страшновато, но стоит все чуть обозначить иначе и оказывается, что ничего страшного нет. Если обозначить через С; амплитуду того, что состояние y находится в базисном состоянии iS , т. е. C i = < iS | y >, а через C ' j назвать соответствующие амплитуды для базисной системы Т. т. е. С j =< jT | y >, то (4.4) можно записать в виде

где R ji — то же самое, что и < jT | iS > . Каждая амплитуда C j есть сумма по всем i одного ряда коэффициентов R ji , умно­женных на каждую амплитуду С i . Это выглядит так же, как преобразование вектора от одной системы координат к другой.