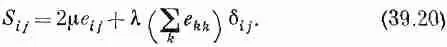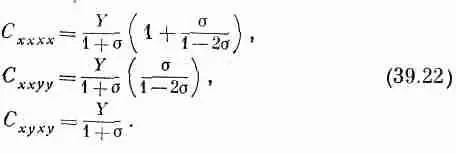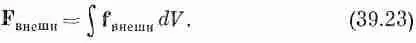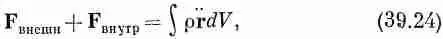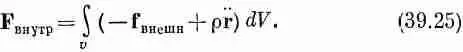Feynmann - Feynmann 7

C хххх = C ххуу + C хуху (39.19)

Это можно усмотреть из следующих общих рассуждений. Тен­зор напряжений S ij должен быть связан с e ij способом, который совершенно не зависит от направления осей координат, т. е. он должен быть связан только с помощью скалярных величин. «Это очень просто»,— скажете вы. «Единственный способ полу­чить S ij из e ij — умножить последнее на скалярную постоянную. Получится как раз закон Гука: S ij = (Постоянная)Xе ij». Однако это не совсем верно. Дополнительно здесь можно вста­вить единичный тензор d ij , умноженный на некоторый скаляр, линейно связанный с е ij . Единственный инвариант, который можно составить и который линеен по е, — это Se jj . (Он преоб­разуется подобно х 2 +y 2+z 2, а значит является скаляром.) Таким образом, наиболее общей формой уравнения, связывающего S ij с e ij для изотропного материала, будет

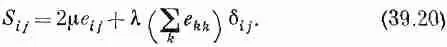
(Первая константа обычно записывается как 2m; при этом коэффициенту равен модулю сдвига, определенному нами в пре­дыдущей главе.) Постоянные (m, и l называются упругими по­стоянными Лямэ. Сравнивая уравнения (39.20) с уравнением (39.12), вы видите, что

Таким образом, мы доказали, что уравнение (39.19) действи­тельно правильное. Вы видите также, что упругие свойства изотропного материала, как уже говорилось в предыдущей главе, полностью задаются двумя постоянными.

Коэффициенты С могут быть выражены через любые две из упругих постоянных, которые использовались ранее, напри­мер через модуль Юнга Y и отношение Пуассона s . На вашу долю оставляю показать, что

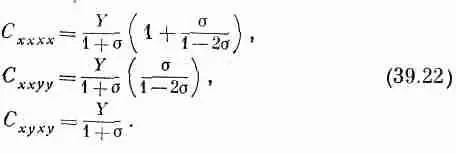
§ 3. Движения в упругом теле

Мы подчеркивали, что в упругом теле, находящемся в равно­весии, внутренние напряжения распределяются так, чтобы энергия была минимальной. Посмотрим теперь, что происходит, если внутренние силы не уравновешены. Возьмем маленький кусочек материала внутри некоторой поверхности А (фиг. 39.5).

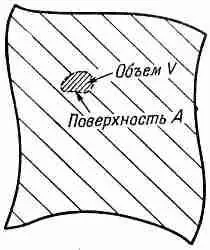
Фиг. 39.5. Маленький элемент объема V , ограниченный поверхностью А,

Если этот кусочек находится в равновесии, то полная действую­щая на него сила F должна быть равна нулю. Можно считать, что эта сила состоит из двух частей, одна из которых обуслов­лена «внешними» силами, подобными гравитации, действующими на расстоянии на вещество нашего кусочка и приводящими к величине силы на единицу объема f внешн. Полная же внешняя сила F внешнравна интегралу от f внешнпо всему объему кусочка:

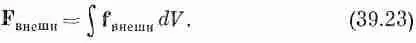
В равновесии эти силы балансируются полной силой F внутр, действующей по поверхности А со стороны окружающего материала. Когда же этот кусочек не на­ходится в равновесии, а движется, сум­ма внутренних и внешних сил будет равна произведению массы на ускорение. При этом мы получаем

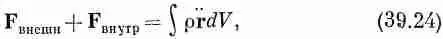
где r—плотность материала, а а— его ускорение. Теперь мы можем скомбинировать уравнения (39.23) и (39.24) и написать

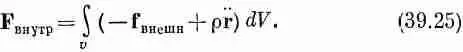
Нашу запись можно упростить, положив

Тогда уравнение (39.25) запишется в виде

Величина, названная нами F внутр, связана с напряжениями в материале. Тензор напряжений S ij был определен нами в гл. 31 таким образом, что x-компонента силы dF , действующей на эле­мент поверхности da с нормалью n, задается выражением