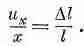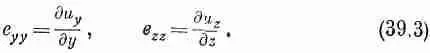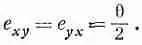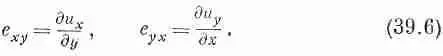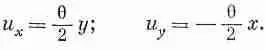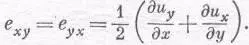Feynmann - Feynmann 7

Сначала рассмотрим простейший случай, ког­да деформация по всему материалу постоянна, т. е. то, что называется однородной деформацией. Предположим, например, что мы взяли балку из како­го-то материала и равномерно ее растянули. Иначе говоря, мы просто равномерно изменили ее размер в одном направле­нии, скажем в направлении оси х (фиг. 39.2).

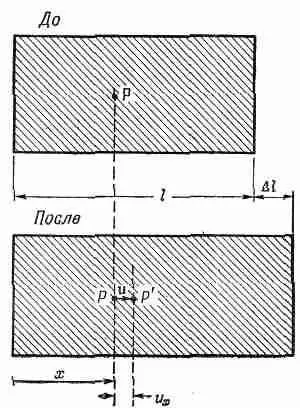
Фиг. 39.2. Однородная деформация растяжения.

Перемещение u x пятнышка с координатой х пропорционально самому х.

Действительно,

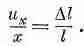
Мы будем записывать u x следующим образом:

и x =е хх х .

Разумеется, константа пропорциональности е хх — это то же, что наше старое отношение Dl/l. (Скоро вы увидите, почему нам потребовался двойной индекс.)

Если же деформация неоднородна, то связь между х и u x в материале будет изменяться от точки к точке. В таком общем случае мы определим е хх как своего рода локальную величину Dl/l, т. е.

Это число, которое теперь будет функцией х, у и z, описывает величину растяжения в направлении оси х по всему куску желе. Возможны, конечно, растяжения и в направлении осей у и z . Мы будем описывать их величинами

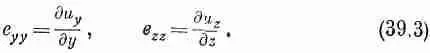
Кроме того, нам нужно описать деформации типа сдви­гов. Вообразите, что в перво­начально невозмущенном желе вы выделили маленький кубик. Нажав на желе, мы изменяем его форму, и наш кубик может превратиться в параллелограмм (фиг. 39.3).

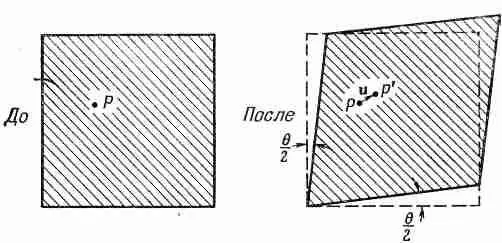
Фиг. 39.3. Однородная деформация сдвига.

При такой дефор­мации перемещение в направлении х каждой частицы пропорционально ее координате у:

а перемещение в направлении у пропорционально х:

u y=(q/2)x. (39.5)

Таким образом, деформацию сдвигового типа можно описать с помощью

u x=e xy y u у = e yx x,

где

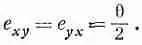
Теперь вы сочтете, что при неоднородной деформации обоб­щенную деформацию сдвига можно описать, определив вели­чины е xy и е yx следующим образом:

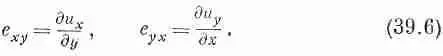
Однако здесь есть некая трудность. Предположим, что пере­мещения u х и u y имеют вид

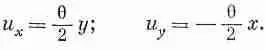
Они напоминают уравнения (39.4) и (39.5), за исключением того, что при u y стоит обратный знак. При таком перемещении маленький кубик из желе претерпевает простой поворот на угол q/2 (фиг. 39.4).

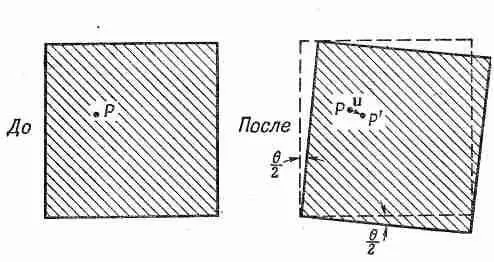
Фиг. 39.4. Однородный поворот. Никаких деформаций нет.

Никакой деформации здесь вообще нет, а есть просто вращение в пространстве. При этом никакого возмущения материала не происходит, а относительное поло­жение всех атомов совершенно не изменяется. Нужно как-то устроить так, чтобы чистое вращение не входило в наше опре­деление деформации сдвига. Указанием может послужить то, что если д u y /дх и д u x /ду равны и противоположны, никакого напряжения нет; этого можно добиться, определив

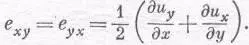
Для чистого вращения оба они равны нулю, но для чистого сдвига мы получаем, как и хотели, е ху =е у x .