Feynmann - Feynmann 7

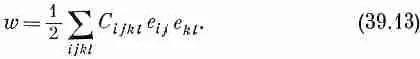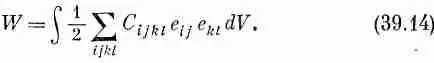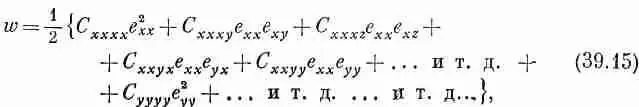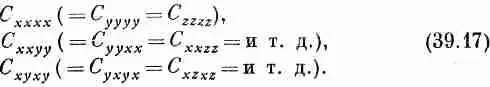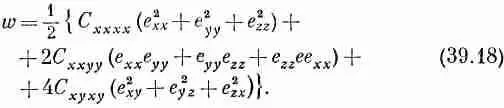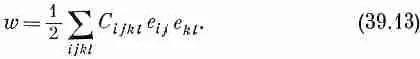
Полная же работа W , затраченная на деформацию всего тела, будет интегралом от w по всему его объему:

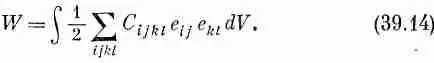
Следовательно, это и есть потенциальная энергия, запасенная во внутренних напряжениях материала. Когда тело находится в равновесии, эта внутренняя энергия должна быть минималь­ной. Таким образом, проблема определения деформаций в теле может быть решена нахождением таких перемещений и по всему телу, при которых W минимальна. В гл. 19 (вып. 6) я го­ворил вам о некоторых общих идеях вариационного исчисле­ния, применяемого при решении задач на минимизацию подоб­ного рода. Однако сейчас мы больше не будем вдаваться в под­робности этой задачи.

Сейчас нас главным образом будет интересовать то, что можно сказать относительно общих свойств тензора упругости. Прежде всего ясно, что на самом деле в C ijkl содержится не 81 различный параметр. Поскольку S ij и e ij — симметричные тензоры, каждый из которых включает только шесть различных элементов, то C ijkl состоит максимум из 36 различных компо­нент. Обычно же их гораздо меньше.

Рассмотрим специальный случай кубического кристалла. Плотность энергии w для него получается такой:

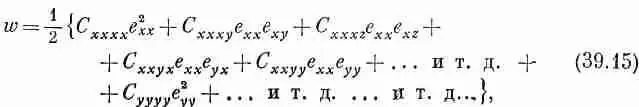
т. е. всего 81 слагаемое! Но кубический кристалл обладает определенными симметриями. В частности, если кристалл по­вернуть на 90°, то все его физические свойства останутся теми же. Например, у него должна быть одна и та же жесткость относительно растяжения как в направлении оси у, так и в нап­равлении оси х. Следовательно, если мы переменим наши опре­деления осей координат х и у в уравнении (39.15), то энергия не должна измениться. Поэтому для кубического кристалла

C хххх = С уууу = C zzzz . (39.16)

Мы можем еще показать, что компоненты, наподобие С ххху , должны быть нулями. Кубический кристалл обладает тем свой­ством, что он симметричен при отражении относительно любой плоскости, перпендикулярной к одной из осей координат. Если мы заменим у на —y, то ничего не должно измениться. Но из­менение у на - у меняет е xy на - е xy , так как перемещение в нап­равлении + у будет теперь перемещением в направлении - у. Чтобы энергия при этом не менялась, С ххху должно переходить в - С ххху Но отраженный кристалл будет тем же, что и прежде, поэтому С хх xy должно быть таким же, как и - С ххху . Это может произойти только тогда, когда оба они равны нулю.

Но вы можете сказать: «Рассуждая таким же образом, можно сделать и C yyyy =0! » Это неверно. Ведь здесь у нас четыре игрека. Каждый у изменяет знак, а четыре минуса дают плюс. Если у встречается два или четыре раза, то такие компоненты не должны быть равны нулю. Нулю равны только те компо­ненты, у которых у встречается либо один, либо три раза. Таким образом, для кубического кристалла не равны нулю только те С, у которых один и тот же значок встречается четное число раз. (Рассуждения, которые мы провели для у, имеют силу и для х и для z.) Таким образом, выживают только компоненты типа С ххуу , С хуху , С хуух и т. д. Однако мы уже показали, что если изменить все х на у и наоборот (или все z на x и т. д.), то для кубического кристалла мы должны получить то же самое число. Это означает, что остаются всего три различные ненуле­вые возможности:

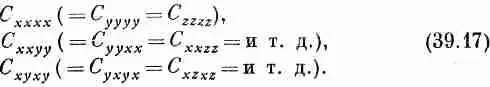
Плотность же энергии для кубического кристалла выглядит так:

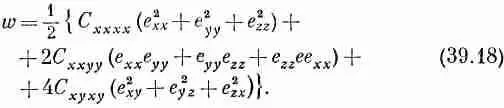
У изотропного, т. е. некристаллического, материала симмет­рия еще выше. Числа С должны быть теми же самыми при любом выборе осей координат. При этом, как оказывается, существует другая связь между коэффициентами С: