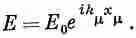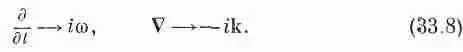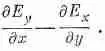Feynmann - Feynmann 7

§ 2. Волны в плотных материалах

Прежде всего я напомню вам об удобном способе описания синусоидальных плоских волн, которым мы пользовались в гл. 36 (вып. 3). Любая компонента поля в волне (возьмем, на­пример, Е) может быть записана в форме

E=E 0e i ( w t - k · r ), (33.6)

где Е — амплитуда поля в точке г (относительно начала коор­динат) в момент t . Вектор kуказывает направление распростра­нения волны, а его величина | k|=k=2pl равна волновому числу. Фазовая скорость волны v фаз=w/k для света в материале с показателем n будет равна c/n, поэтому

k = w n / c . (33.7)

Предположим, что вектор kнаправлен по оси z; тогда k · r будет просто хорошо знакомым нам kz . Для вектора kв любом другом направлении z следует заменить на r k — расстояние от начала в направлении вектора k, т. е. kz мы должны заменить на kr k , что как раз равно k · r (фиг. 33.2).

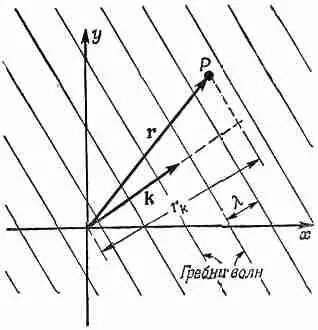
Фиг. 33.2. Фаза волны в точке Р, распространяющейся в направ­лении k , равна ( w t - k · r ).

Таким образом, запись (33.6) является удобным представлением волны, идущей в любом направлении.

Разумеется, при этом мы должны помнить, что

k · r = k x x + k y y + k : z z ,

где k x , k y и k z — компоненты вектора kпо трем осям. Мы уже отмечали однажды, что на самом деле величины (w, k x , k y , k z ) образуют четырехвектор и что его скалярное произведение на ( t , x , у, z ) является инвариантом. Таким образом, фаза волны есть инвариант и формулу (33.6) можно записать в виде

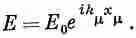
Однако сейчас нам такие хитрости не понадобятся.

Для синусоидального по­ля Е, подобного выражению (33.6), производная dE / д t — это то же самое, что и i w E , a дЕ/дх — то же, что и ik x E , и аналогично для остальных компо­нент. Вы видите, чем удобна форма (33.6): когда мы работаем с дифференциальными уравнениями, то дифференцирование заменяется простым умножением. Другое полезное качество состоит в том, что операция С =( д / д x ), (д/ду), ( д / д z ) заменяется тремя умножениями (- ik x ,- ik y , - ik z ). Но эти три множителя преобразуются как компоненты вектора k, так что оператор С заменяется умножением на

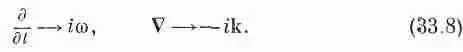
Правило остается справедливым для операции С в любой ком­бинации, будь то градиент, дивергенция или ротор. Например, z-компонента СX Еравна

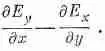
Если и Е у и Е х изменяются как e - i k · r , то мы получаем

- ik x E y + ik y E x ,

что представляет, как вы видите, z-компоненту —i kX Е.

Таким образом, мы получили очень полезный общий закон, что в любом случае, когда вам нужно взять градиент от вектора, который изменяется, как волна в трехмерном пространстве (а они в физике играют важную роль), эту операцию вы можете проделать быстро и почти без всяких раздумий, если вспомните, что оператор С эквивалентен умножению на —i k.

Например, уравнение Фарадея

СX Е= д B/ д t

превращается для волны в

— i kX Е=-iw B. Оно говорит, что

В= kX E/w. (33.9)

Это соответствует результату, найденному ранее для волн в пу­стом пространстве, т. е. что вектор Вв волне направлен под прямым углом к вектору Еи направлению распространения волны. (В пустом пространстве w/k=с.) Знак в уравнении (33.9) вы можете проверить, исходя из того, что kявляется на­правлением вектора Пойнтинга S=e 0c 2( EX В).