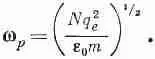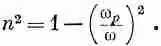Feynmann - Feynmann 7

что, разумеется, эквивалентно уравнению (32.50). Раньше нам

уже встречалась величина ( Nq 2 e / e 0 m ) 1/2 , которую мы назвали

плазменной частотой (см. гл. 7, § 3, вып. 5);

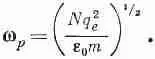
Таким образом, (32.50) или (32.51) можно переписать в виде

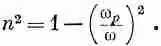
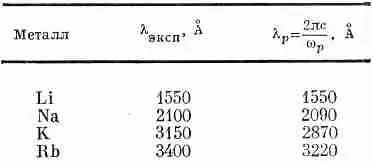
Эта плазменная частота является своего рода «критической». Для wрпоказатель преломления металла имеет мнимую часть и происходит поглощение волн, но при w>>w pпоказатель становится вещественным, а металл — прозрачным. Вы знаете, конечно, что металлы в достаточной мере прозрачны для рент­геновских лучей. Но некоторые металлы прозрачны даже для ультрафиолета. В табл. 32.3 мы приводим для некоторых ме­таллов экспериментально наблюдаемые длины волн, при кото­рых эти металлы начинают становиться прозрачными. Во второй колонке дана вычисленная критическая длина волны l p=2pc/w p. Учитывая, что экспериментальная длина волны определена не очень хорошо, согласие с теорией следует приз­нать замечательным.

Таблица 32.3 · длины волн, при ко­торых МЕТАЛЛ СТАНО­ВИТСЯ ПРОЗРАЧНЫМ

Вас может удивить, почему плазменная частота w рдолжна иметь отношение к распространению волн в металлах. Плаз­менная частота появилась у нас в гл. 7 (вып. 5) как собственная частота колебаний плотности свободных электронов. (Электри­ческое расталкивание группы электронов и их инерция приво­дят к колебаниям плотности.) Продольные волны плазмы резо­нируют при частоте w. Но сейчас мы говорим о поперечных вол­нах, и мы уже нашли, что при частотах, меньших w р , происхо­дит их поглощение. (Это очень интересное и отнюдь не случайное совпадение.)

Хотя мы все время говорили о распространении волн в ме­таллах, вы одновременно, должно быть, почувствовали универ­сальность явлений физики: нет никакой разницы в том, находят­ся ли свободные электроны в металле, в плазме, в ионосфере Земли или в атмосфере звезд. Чтобы понять распространение радиоволн в ионосфере, можно воспользоваться тем же выраже­нием, разумеется, при надлежащих значениях величин N и t. Теперь мы можем видеть, почему длинные радиоволны погло­щаются или отражаются ионосферой, тогда как короткие сво­бодно проходят через нее. (Поэтому для связи с искусственными спутниками Земли должны применяться короткие волны.)

Мы говорили о распространении предельных высоко- и низ­кочастотных волн в металлах. Для промежуточных же частот необходимо использовать «полновесное» уравнение (32.42). В общем случае показатель преломления будет иметь веществен­ную и мнимую части, и при распространении волн в металлах происходит их поглощение. Очень тонкие слои металла про­зрачны даже для обычных оптических частот. В качестве примера приведем специальные защитные очки для рабочих, работаю­щих около высокотемпературных печей. Эти очки изготавли­ваются напылением на стекло очень тонкого слоя золота; стекло это достаточно прозрачно для видимого света и на просвет выглядит как зеленое, но инфракрасные лучи сильно поглощает.

И, наконец, от читателя невозможно скрыть тот факт, что многие из этих формул в некотором отношении напоминают формулы для диэлектрической проницаемости c , рассмотренные в гл. 10 (вып. 5). Диэлектрической проницаемостью c измеряется реакция материала на статическое электрическое поле, т. е. когда w=0. Если вы посмотрите повнимательнее на определе­ние n и c , то обнаружите, что c есть не что иное, как предел n 2при w®0. В самом деле, положив в уравнениях этой главы w=0 и n 2=c , мы воспроизведем уравнения теории диэлектри­ческой проницаемости гл. 11 (вып. 5).

* Или записав — i =е - i p / 2 ; Ц - i = e - i p /4 = со s p /4 - isin p /4, что приводит к тому же результату.