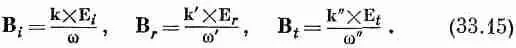Feynmann - Feynmann 7

Если вы примените то же самое правило к другим уравне­ниям Максвелла, то снова получите результаты последней главы, в частности

Но раз уже это известно нам, давайте не будем проделывать все сначала.

Если вы хотите поразвлечься, можете попытаться решить та­кую устрашающую задачу (в 1890 г. она предлагалась студен­там на выпускных экзаменах): решите уравнения Максвелла для плоской волны в анизотропном кристалле, т. е. когда поля­ризация Рсвязана с электрическим полем Ечерез тензор поля­ризуемости. Конечно, в качестве ваших осей вы выберете глав­ные оси тензора, так что связи при этом упростятся (тогда Р х = a a Е х , Р у = a b Е у , a P z = a c E z ), но направление волны и ее поляризация пусть останутся произвольными. Вы должны найти соотношение между Еи Ви определить, как изменяется k с направлением распространения волны и ее поляризацией. После этого вам будет понятна оптика анизотропного кристалла. Лучше начать с более легкого случая дважды лучепреломляющего кристалла, подобного турмалину, для которого два коэффи­циента поляризуемости равны между собой (например, a b = a c ), и попытаться понять, почему, когда мы смотрим через такой кристалл, мы видим два изображения. Если это вам удастся, тогда испытайте свои силы на более трудном случае, когда все три а различны. После этого вам уже будет ясен уровень ваших знаний — знаете ли вы столько же, сколько студент, заканчи­вавший университет в 1890 г. Но мы с вами в этой главе будем рассматривать только изотропные вещества.

Из опыта вам известно, что когда на границу раздела двух материалов, скажем воздуха и стекла или воды и бензина, попадает плоская волна, то возникают как отраженная, так и преломленная волны.

Предположим, что, кроме этого факта, нам больше ничего неизвестно, и посмотрим, что можно из него вывести. Выберем наши оси так, чтобы плоскость yz совпадала с поверхностью раздела, а плоскость ху была перпендикулярна фронту волны (фиг. 33.3).

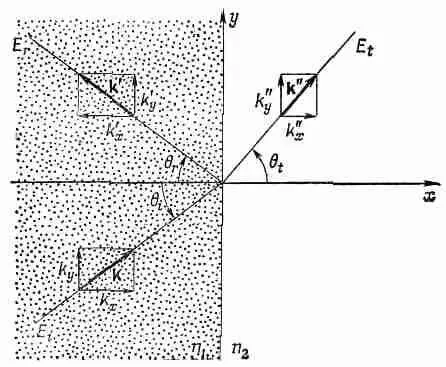
Фиг. 33.3. Векторы, распространения k, k' и k" для падающей, отраженной и прелом­ленной волн.

Электрический вектор в падающей волне может быть записан в виде

Поскольку вектор kперпендикулярен оси z, то

k · r = k x x + k y y . (33.12) Отраженную волну мы запишем как

так что ее частота равна w', волновое число k ',а амплитуда Е' 0. (Мы, конечно, знаем, что частота и величина вектора kв отра­женной волне те же, что и в падающей волне, но не хотим пред­полагать даже это. Пусть это все получится само собой из мате­матического аппарата.) Наконец, запишем преломленную волну:

Вы знаете, что одно из уравнений Максвелла дает соотноше­ние (33.9), так что для каждой из волн

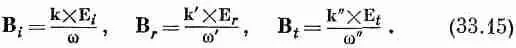
Кроме того, если показатели преломления двух сред мы обозна­чим через n 1 и n 2, то из уравнения (33.10) получится

Поскольку отраженная волна находится в том же ма­териале, то

в то время как для преломленной волны

§ 3. Граничные условия