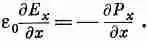Feynmann - Feynmann 7

Предположим, например, что у нас есть граница между вакуумом (область 1) и стеклом (область 2). В вакууме нечему поляризоваться, так что P 1=0. А поляризация в стекле пусть равна Р 2 .Между вакуумом и стеклом существует гладкий, но быстрый переход. Если мы проследим за какой-то компонентой Р, скажем Р х , то она может изменяться так, как это показано на фиг. 33.5, а.

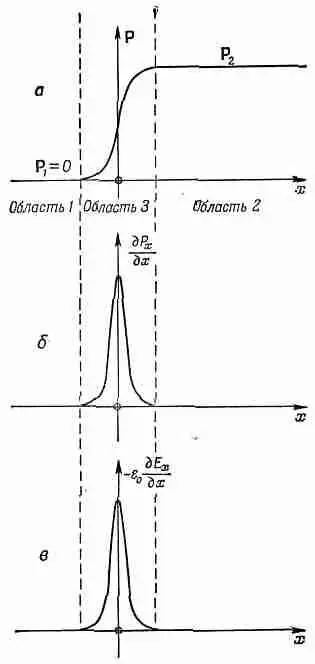
Фиг. 33.5. Поля в переходной об­ласти 3 между двумя различными материалами в областях 1 и 2.

Предположим теперь, что мы взяли первое из наших уравнений — уравнение (33.21). В него входит производ­ная от компонент Рпо переменным х, у и z. Производные по у и r не очень интересны — в этих направлениях не происходит ничего замечательного. Но производная от Р х по х в области 3 из-за быстрого изменения Р х будет громадна. Производная дР х /дх, как показано на фиг. 33.5,б, имеет на границе очень резкий пик. Если вы представите, что граница сжимается до еще более тонкой области, пик вырастет еще больше. Если для интересующих нас волн граница действительно резкая, то ве­личина д P / д x в области 3 будет больше, много больше любого вклада, который может получиться из-за изменения Р в сто­роне от границы, так что мы пренебрегаем любыми другими изменениями, за исключением происходящих на границе.

Но как теперь можно удов­летворить уравнению (33.21), если с правой стороны у нас возвышается огромный пик? Только если существует рав­ный ему громадный пик с другой стороны. Что-то и с левой стороны должно быть большим. Единственная воз­можность — это дЕ х /дх, пос­кольку изменения в направ­лениях у и z в тех волнах, о которых мы только что упо­мянули, дают лишь малый эффект. Таким образом, -e 0 (дЕ х /дх) должно быть, как это показано на фиг. 33.5,в, точной копией д P / д x . Получается

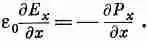
Если это уравнение проинтегрировать по х по всей области 3, то мы придем к заключению, что

e 0 (Е x 2 -Е x 1 )= - (Р x 2 -Р x 1 ). (33.25)

Другими словами, скачок e 0 Е х при переходе от области 1 к об­ласти 2 должен быть равен скачку — Р х .

Уравнение (33.25) можно переписать в виде

e 0E x 2+Р x 2=e 0E x 1+Р x 1; (33.26)

оно гласит, что величина (e 0E x+Р x) имеет равные значения как в области 2, так и в области 1. В таких случаях люди гово­рят, что величина ( e 0 Е x + Р х ) непрерывна на границе. Таким образом, мы получили одно из наших граничных условий.

Хотя в качестве иллюстрации мы взяли случай, когда зна­чение Р 1равно нулю, ибо в области 1 у нас был вакуум, ясно, что те же аргументы приложимы для любого материала в этих двух областях, так что уравнение (33.26) верно в общем случае. Давайте перейдем к остальным уравнениям Максвелла и по­смотрим, что скажет нам каждое из них. Следующим мы возьмем уравнение (33.22а). У него нет производной по х, так что оно ничего нам не говорит. (Вспомните, что на границе сами поля не особенно велики. Только их производные по х могут стать столь огромными, что будут доминировать в уравнении.) Взгля­нем теперь на уравнение (33.22.б). Смотрите! Именно здесь у нас есть производная по х ! С левой стороны имеется д E z / д x . Пред­положим, что эта производная громадна. Но минуточку терпе­ния! С правой стороны нет ничего, способного потягаться с ней, поэтому Е z не может иметь скачка при переходе из области 1 к области 2. [Если бы это было так, то с левой стороны уравне­ния (33.22а) мы бы получили скачок, а с правой — его не было бы, и уравнение оказалось бы неверным.] Итак, мы получили новое условие:

E я2 = E я1 . (33.27)

После тех же самых рассуждений уравнение (33.22в) дает

E y 2 = E y 1 . (33.28)

Последний результат в точности совпадает с полученным с по­мощью контурного интеграла условием (33.20).

Перейдем к уравнению (33.23). Единственное, что может дать пик,— это дВ х /дх. Но справа опять нет ничего, способного противостоять ему; в результате мы заключаем, что