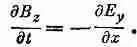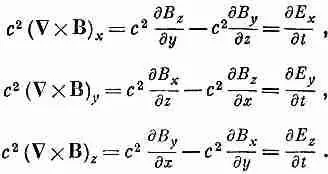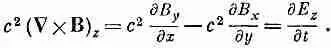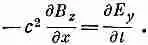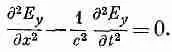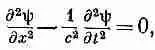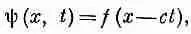Feynmann - Feynmann 6

здесь x-компонента СXE равна нулю, потому что равны нулю производные по у и z; y-компонента тоже равна нулю: первый член потому, что все производные по z равны нулю, а второй потому, что E z =0. Единственная не равная нулю компонента rot E — это z-компонента, она равна дЕ у /дх. Полагая, что три компоненты СXE равны соответствующим компонентам — dB / dt , мы заключаем, что

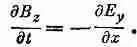
(20.15)

(20.16)

Поскольку временные производные как x-компоненты магнит­ного поля, так и

y-компоненты магнитного поля равны нулю, то обе эти компоненты суть попросту постоянные поля и отве­чают найденным раньше магнитостатическим решениям. Ведь кто-то мог оставить постоянный магнит возле того места, где распространяются волны. Мы будем игнорировать эти по­стоянные поля и положим В х и В y равными нулю.

Кстати, о равенстве нулю x-компонент поля В мы должны были бы заключить и по другой причине. Поскольку диверген­ция В равна нулю (по третьему уравнению Максвелла), то мы, прибегая при рассмотрении электрического поля к тем же доводам, что и выше, должны были бы прийти к выводу, что продольная компонента магнитного поля не может изменяться вдоль х. А раз мы такими однородными полями в наших вол­новых решениях пренебрегаем, то нам следовало бы положить В х равным нулю. В плоских электромагнитных волнах поле В, равно как и поле Е, должно быть направлено поперек направ­ления распространения самих волн.

Равенство (20.16) дает нам добавочное утверждение о том, что если электрическое поле имеет только y-компоненту, то магнитное поле имеет только z-компоненту. Значит, Е и В перпендикулярны друг другу. Именно это и наблюдалось в той волне особого типа, которую мы уже рассмотрели.

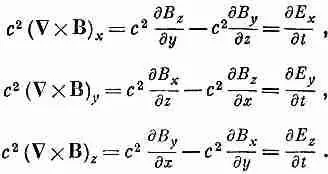
Теперь мы готовы использовать последнее из уравнений Максвелла для пустого пространства [т. е. IV из (20.12)1. Рас­писывая покомпонентно, имеем

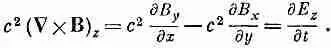
(20.17)

Из шести производных от компонент В только dB z / dx не равна нулю. Так что три уравнения просто дают

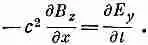
(20.18)

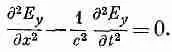
Итог всей нашей деятельности состоит в том, что отличны от нуля только по одной компоненте электрического и магнит­ного полей и эти компоненты обязаны удовлетворять уравне­ниям (20.16) и (20.18). Эти два уравнения можно объединить в одно, если первое из них продифференцировать по х, а второе— по t ; тогда левые стороны уравнений совпадут (с точностью до множителя с 2). И мы обнаруживаем, что Е подчиняется урав­нению

(20.19)

Мы уже встречали это дифференциальное уравнение, когда изучали распространение звука. Это волновое уравнение для одномерных волн.

Заметьте, что в процессе вывода мы получили больше, чем содержится в (20.11). Уравнения Максвелла дали нам ин­формацию и о том, что у электромагнитных волн есть только компоненты поля, расположенные под прямым углом к направ­лению распространения волн.

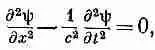
Вспомним все, что нам известно о решениях одномерного волнового уравнения. Если какая-то величина ш удовлетво­ряет одномерному волновому уравнению

(20.20)

то одним из возможных решений является функция ш ( x , t ),

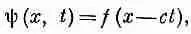
имеющая вид

(20.21)

т. е. функция одной-единственной переменной (x - ct ). Функция i ( x - ct ) представляет собой «жесткое» образование вдоль оси х, которое движется по направлению к положительным х со ско­ростью с (фиг. 20.4). Так, если максимум функции f приходится на нулевое значение аргумента, то при t=0 максимум ш ока­зывается при x=0. В более поздний момент, скажем при t=10, максимум ш окажется в точке х=10 с. Когда время движется, максимум тоже движется в сторону возрастания х со скоростью с. Порой удобнее считать, что решение одномерного волно­вого уравнения является функцией от ( t - х/с). Однако в сущ­ности это одно и то же, потому что любая функция от ( t - х/с)— это