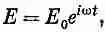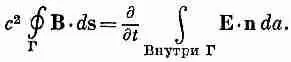Feynmann - Feynmann 6a

Посмотрим теперь повнимательнее на то, что происходит в реальной катушке. Импеданс индуктивности изменяется как w L , значит, он на низких частотах обращается в нуль — «замы­кается накоротко», и мы замечаем только сопротивление прово­да. Если частота начинает расти, то wL вскоре становится боль­ше R и катушка выглядит почти как идеальная индуктивность. А если подняться по частоте еще выше, то начнут играть роль и емкости. Их импеданс пропорционален 1/wС; он велик на низких частотах. На достаточно низких частотах конденсатор выглядит как «разрыв в цепи», и если его с чем-нибудь запараллелить, то ток через него не пойдет. Но на высоких частотах ток предпочитает течь через емкости между витками, а не через индуктив­ность. Оттого-то ток в катушке прыгает с одного витка на дру­гой, вовсе не помышляя крутить петлю за петлей там, где ему приходится преодолевать э. д. с. Хоть нам, может быть, и хоте­лось бы, чтобы ток шел по виткам катушки, но сам-то он выби­рает путь полегче, переходя на дорогу наименьшего импеданса. Если это было бы нужно, то такой эффект можно было бы назвать «высокочастотным барьером» или чем-нибудь в этом роде. Похожие вещи происходят и в других науках. В аэродина­мике, скажем, если вы захотите заставить что-то двигаться бы­стрее звука, а движение рассчитано на малые скорости, то у вас ничего не выйдет. Это не значит, что возник какой-то непрохо­димый «барьер»; просто надо изменить конструкцию. Точно так же наша катушка, которую первоначально сконструировали как «индуктивность», на очень высоких частотах работает не как индуктивность, а как что-то другое. Для больших частот надо изобретать уже новое устройство.

§ 2. Конденсатор на больших частотах

А теперь обсудим подробнее поведение конденсатора — гео­метрически идеального конденсатора,—когда частота становится все выше и выше. Мы проследим за изменением его свойств. (Мы предпочли рассматривать конденсатор, а не индуктивность, по­тому что геометрия пары обкладок много проще геометрии ка­тушки.) Итак, вот конденсатор (фиг. 23.4, а), состоит он из двух параллельных круговых обкладок, соединенных с внешним ге­нератором парой проводов. Если зарядить конденсатор посто­янным током, то на одной из обкладок появится положительный заряд, на другой — отрицательный, а между обкладками будет однородное электрическое поле.

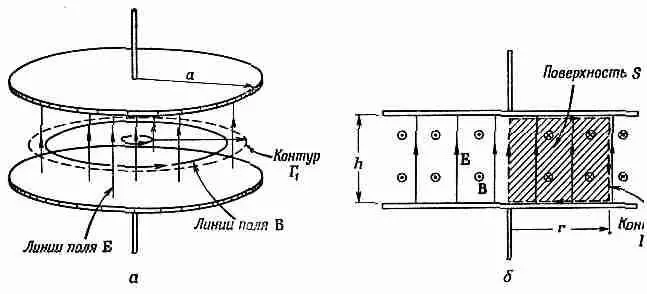
Фиг. 23.4. Электрическое и магнитное поля между обкладками конденсатора.

Представим теперь, что вместо постоянного тока к обкладкам приложено переменное напряжение низкой частоты. (После мы увидим, какая частота «низкая», а какая «высокая».) Конденса­тор, скажем, соединен с низкочастотным генератором. Когда напряжение меняется, то с верхней обкладки положительный заряд убирается и прикладывается отрицательный. В момент, когда это происходит, электрическое поле исчезает, а потом восстанавливается, но уже в обратную сторону. Заряд медленно плещется туда-сюда, и поле поспевает за ним. В каждый момент электрическое поле однородно (фиг. 23.4, б); есть, правда, не­большие краевые эффекты, но мы намерены ими пренебречь. Ве­личину электрического поля можно записать в виде

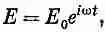
(23.2)

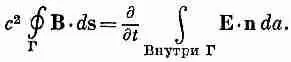
где Е 0 — постоянно. Но останется ли это справедливым, когда частота возрастет? Нет, потому что при движении электрического поля вверх и вниз через произвольную петлю Г 1проходит поток электрического поля (фиг. 23.4, а). А, как вам известно, изменяющееся элект­рическое поле создает магнитное. Согласно одному из уравнений Максвелла, при наличии изменяющегося электрического поля (как в нашем случае) обязан существовать и криволинейный ин­теграл от магнитного поля. Интеграл от магнитного поля по замкнутому кругу, умноженный на с 2, равен скорости измене­ния во времени электрического потока через поверхность внутри круга (если нет никаких токов):

(23.3)

Итак, сколько же здесь этого магнитного поля? Это узнать не­трудно. Возьмем в качестве петли Г 1круг радиуса r. Из симмет­рии ясно, что магнитное поле идет так, как показано на рисун­ке. Тогда интеграл от В равен 2 p r В. А поскольку электрическое поле однородно, то поток его равен просто Е, умноженному на pr 2, на площадь круга: