Feynmann - Feynmann 6a

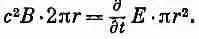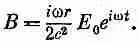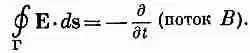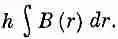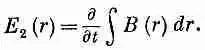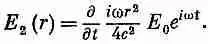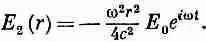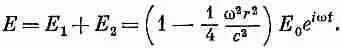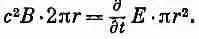
(23.4)

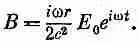
Производная Е по времени в нашем переменном поле равна i w E 0 e i w t , Значит, в нашем конденсаторе магнитное поле равно

(23.5)

Иными словами, магнитное поле тоже колеблется, а его величи­на пропорциональна w и r.

К какому эффекту это приведет? Когда существует магнит­ное поле, которое меняется, то возникнут наведенные электри­ческие поля, и действие конденсатора станет слегка похоже на индуктивность. По мере роста частоты магнитное поле усилива­ется: оно пропорционально скорости изменения Е, т. е. w. Им­педанс конденсатора больше не будет просто равен 1/ i w С.

Будем увеличивать частоту и посмотрим повниматель­нее, что происходит. У нас есть магнитное поле, которое пле­щется то туда, то сюда. Но тогда и электрическое поле не может, как мы раньше предполагали, остаться однородным! Если имеет­ся изменяющееся магнитное поле, то по закону Фарадея должен существовать и контурный интеграл от электрического поля. Так что если существует заметное магнитное поле (а так и бы­вает на высоких частотах), то электрическое поле не может быть на всех расстояниях от центра одинаковым. Оно должно так меняться с r , чтобы криволинейный интеграл от него мог быть равен изменяющемуся потоку магнитного поля.

Посмотрим, сможем ли мы представить себе правильное электрическое поле. Это можно сделать, подсчитав «поправку» к тому, что было на низких частотах,— к однородному полю. Обозначим поле при низких частотах через Е 1 , и пусть оно по-прежнему равно Е 0 е i w t , а правильное поле запишем в виде

где E 2 — поправка из-за изменения магнитного поля. При любых w мы будем задавать поле в центре конденсатора в виде E 0 e i w t (тем самым определяя Е 0 ), так что в центре поправки не будет: E 2=0 при r=0.

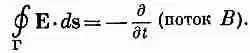
Чтобы найти Е 2 , можно использовать интегральную форму закона Фарадея

Интегралы берутся просто, если вычислять их вдоль линии Г 2, показанной на фиг. 23.4,б и идущей сперва по оси, затем по радиусу вдоль верхней обкладки до расстояния r, потом вер­тикально вниз на нижнюю обкладку и обратно к оси по радиусу. Контурный интеграл от Е 1 вдоль этой кривой, конечно, равен нулю; значит, в интеграл дает вклад только Е 2 , и интеграл равен просто — E z ( r ) h , где h — зазор между обкладками. (Мы считаем Е положительным, когда оно направлено вверх.) Это равно скорости изменения потока В, который получится, если вычислить интеграл по заштрихованной площади S внутри Г 2(фиг. 23.4,6). Поток через вертикальную полосу шириной dr равен B ( r ) hdr , а суммарный поток

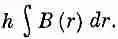
Полагая — d / dt от потока равным контурному интегралу от E 2, получаем

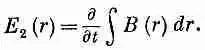
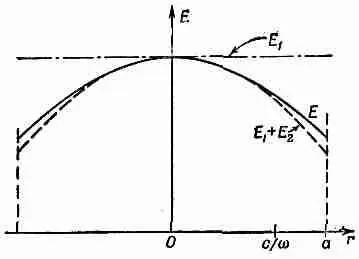
Фиг. 23.5. Электрическое по­ле между обкладками конден­сатора на высоких частотах. Краевыми аффектами пренебрегли.

Заметьте, что h выпало: поля не зависят от величины зазора между обкладками.

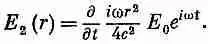
Используя для В( r ) формулу (23.5), получаем

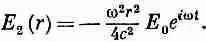
Дифференцирование по времени даст нам просто еще один множитель i w :

(23.7)

Как и ожидалось, наведенное поле стремится свести на нет первоначальное электрическое поле. Исправленное поле Е = Е 1 + Е 2 тогда равно

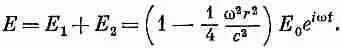
(23.8)

Электрическое поле в конденсаторе больше уже не однород­но; оно имеет параболическую форму (штриховая линия на фиг. 23.5). Вы видите, что наш простенький конденсатор уже слегка усложняется.