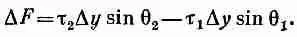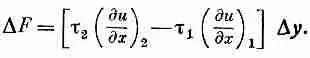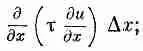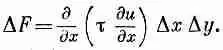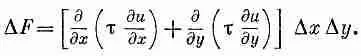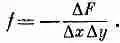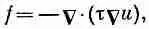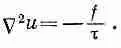Feynmann - Feynmann 5b

Возьмем небольшой кусочек поверхности длиной Dx; и ши­риной Dу. На него действуют силы вследствие поверхностного натяжения вдоль каждого края. Сила на стороне 1 (см. фиг. 12.5) будет равна t 1Dy и направлена по касательной к поверхности, т. е. под углом q 1к горизонтали. Вдоль стороны 2 сила будет равна t 2Dy и направлена к поверхности под углом q 2. (Подобные силы будут и на двух других сторонах кусочка, но мы пока забудем о них.) Результирующая сила от сторон 1 и 2, дей­ствующая на кусочек вверх, равна

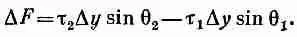
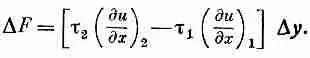
Мы ограничимся рассмотрением малых искажений мембраны, т. е. малых изгибов и наклонов: тогда мы сможем заменить sinq на tgq и записать как д u /д x . Сила при этих условиях дается выражением

Величина в скобках может быть с тем же успехом записана (для малых Dx:) как

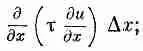
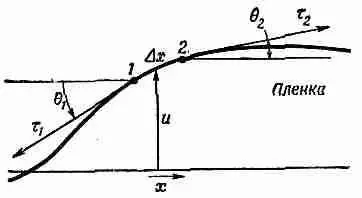
Фиг. 12.5. Поперечное сечение изогнутой пленки.

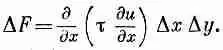
Тогда

Имеется и другой вклад в D F от сил на двух других сторо­нах; полный вклад, очевидно, равен

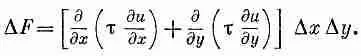
(12.16)

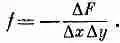
Искривления диафрагмы вызваны внешними силами. Пусть / означает направленную вверх силу на единичную площадку пленки (своего рода «давление»), возникающую от внешних сил. Если мембрана находится в равновесии (статический случай), то сила эта должна уравновешиваться только что вычисленной внутренней силой [уравнение (12.16)]. Иначе говоря,

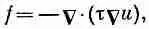
Уравнение (12.16) тогда может быть записано в виде

(12.17)

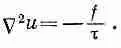
где под знаком С мы теперь подразумеваем, конечно, двух­мерный оператор градиента (д/дх, д/ду). У нас есть дифферен­циальное уравнение, связывающее u (х, у) с приложенными си­лами f ( x , у) и поверхностным натяжением пленки t ( x , у), которое, вообще говоря, может меняться от места к месту. (Деформации трехмерного упругого тела тоже подчиняются таким уравнениям, но мы ограничимся двухмерным случаем.) Нас будет интересовать только случай, когда натяжение t постоянно по всей пленке. Тогда вместо (12.17) мы можем запи­сать

(12.18)

Снова мы получили такое же уравнение, как в электроста­тике! Но на сей раз оно относится к двум измерениям. Сме­щение u соответствует j, а f/t соответствует r/e 0. Поэтому тот труд, который мы потратили на бесконечные заряженные плос­кости, или параллельные провода большой длины, или заряжен­ные цилиндры, пригодится для натянутой мембраны.

Предположим, мы подтягиваем мембрану в каких-то точках на определенную высоту, т. е. фиксируем величину и в ряде точек. В электрическом случае это аналогично заданию определенного потенциала в соответствующих местах. На­пример, мы можем устроить положительный «потенциал», если подопрем мембрану предметом, который имеет такое же сечение, как и соответствующий цилиндрический проводник. Если, скажем, мы подопрем мембрану круглым стержнем, поверхность примет форму, изображенную на фиг. 12.6.

Фиг. 12.6. Поперечное сечение натянутой рези­новой пленки, подпертой круглым стержнем.

Функция u (х, у) та же, что и потенциал j (х, у) от очень длинного заряженного стержня.

Высота и имеет такой же вид, как электростатический потенциал j заряженного цилиндрического стержня. Она спадает, как ln(1/r). (Наклон поверхности, который соответствует электри­ческому полю Е, спадает, как 1/r.)

Натянутую резиновую пленку часто использовали для ре­шения сложных электрических задач экспериментальным путем. Аналогия используется в обратную сторону! Для подъема мембраны на высоту, соответствующую потенциалам всего набора электродов, подставляют разные стержни и полоски. Затем измерения высоты дают электрический потенциал в электростатической задаче. Аналогия проводится даже еще дальше. Если на мембране поместить маленькие шарики, то их движение примерно схоже с движением электронов в соответ­ствующем электрическом поле. Таким способом можно воочию проследить за движением «электронов» по их траекториям. Этот метод был использован для проектирования сложной системы многих фотоумножительных трубок (таких, например, какие используются в сцинтилляционном счетчике или для управления передними фарами в автомашине кадиллак). Метод используется и до сих пор, но его точность не очень велика. Для более точных расчетов лучше находить поле чис­ленным путем с помощью больших электронных вычислитель­ных машин.