Feynmann - Feynmann 5a

Но если внутри проводника не может быть зарядов, как же он вообще может быть заряжен? Что мы имеем в виду, когда говорим, что проводник «заряжен»? Где эти заряды? Они нахо­дятся на поверхности проводника, где существуют большие силы, не дающие им покинуть ее, так что они не вполне «сво­бодны». Когда мы будем изучать физику твердого тела, мы уви­дим, что избыточный заряд в любом проводнике находится толь­ко в узком слое у поверхности, толщиной в среднем в один-два атома. Для наших нынешних целей достаточно правильно будет говорить, что любой заряд, попавший на (или в) проводник, собирается на его поверхности; внутри проводника никаких зарядов нет.

Мы замечаем также, что электрическое поле возле самой поверхности проводника должно быть нормально к поверхности. Касательной составляющей у него быть не может. Если бы она появилась, электроны двигались бы вдоль поверхности; нет сил, которые способны помешать этому. Это можно выразить и иначе: мы знаем, что линии электрического поля должны всег­да быть направлены поперек эквипотенциальной поверхности.

Применяя закон Гаусса, мы можем связать напряженность поля у самой поверхности проводника с локальной плотностью заряда на поверхности. За гауссову поверхность мы примем не­большой цилиндрический стакан, наполовину погруженный в проводник, а наполовину выдвинутый из него (фиг. 5.11). Вклад в общий поток Е дает только та часть стакана, которая находится вне проводника. Тогда поле у наружной поверх­ности проводника равно

Вне проводника:

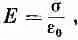
(5.8)

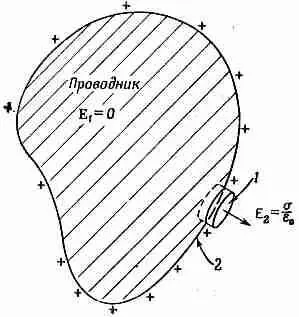
Фиг. 5.11. Электрическое поле у самой внешней поверхности провод­ника пропорционально локальной поверхностной плотности заряда.

1 — гауссова поверхность; 2 — локаль­ная плотность поверхностного заряда.s.

Почему слой зарядов на проводнике создает не такое поле, как слой зарядов сам по себе! Иначе говоря, почему (5.8) вдвое больше (5.3)? Но ведь мы не утверждали, будто в проводнике нет больше никаких «других» зарядов. В действительности для того, чтобы в проводнике Е было равно 0, в нем обязательно должны присутствовать какие-то заряды. В непосредственной близости от точки Р на поверхности заряды действительно соз­дают поле E лок=s лок/2e 0как внутри, так и снаружи поверхно­сти. Но все прочие заряды проводника сообща «устраивают за­говор», чтобы создать в точке Р добавочное поле, равное по величине Е лок . Суммарное внутреннее поле обращается в нуль, а наружное удваивается: 2E лок=s/e 0.

§ 10. Поле внутри полости проводника

Вернемся теперь к проблеме пустотелого резервуара — про­водника, имеющего внутри полость. В металле поля нет, а вот есть ли оно в полости ? Покажем, что если полость пуста, то поля в ней быть не может, какова бы ни была форма провод­ника или полости (фиг. 5.12). Рассмотрим гауссову поверхность, подобную S на фиг. 5.12, которая окружает собой полость, но остается всюду в веществе проводника. Всюду на поверхности S поле равно нулю, так что потока сквозь S быть не может, и суммарный заряд внутри S должен быть равен нулю. Затем можно вывести из симметрии, что на внутренней поверхности сферической оболочки нет никакого заряда. Но в более общем случае мы только можем сказать, что на внутренней поверх­ности проводника имеется равное количество положительного и отрицательного зарядов. Может быть, окажется, что на од­ной части имеется положительный заряд, а где-то в другом месте — отрицательный (см. фиг. 5.12)? Такие вещи законом Гаусса не исключаются.

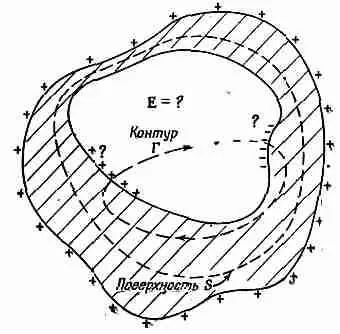
Фиг. 5.12. Чему равно поле в пустой полости проводника произвольной формы?

На самом деле, конечно, получается, что равные, но проти­воположные заряды на внутренней поверхности должны были бы соскользнуть навстречу друг другу и уничтожить друг дру­га. Мы можем убедиться в том, что они уничтожат друг друга, применив закон о равенстве нулю циркуляции Е (электроста­тику). Пусть на каких-то частях внутренней поверхности ока­зались заряды. Мы знаем, что еще где-то должно присутствовать равное количество противоположных зарядов. Но любые ли­нии поля Е начинаются на положительных зарядах и кончаются на отрицательных (мы рассматриваем случай, когда свобод­ных зарядов в полости нет). Представим себе теперь контур Г, пересекающий полость вдоль линии силы от какого-то положи­тельного заряда к какому-то отрицательному и возвращаю­щийся к исходной точке по телу проводника (см. фиг. 5.12). Интеграл вдоль такой линии сил в пределах от положительного до отрицательного заряда не был бы равен нулю, а интеграл по пути через металл