Feynmann - Feynmann 5a

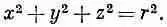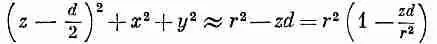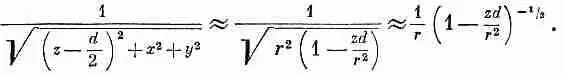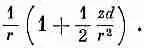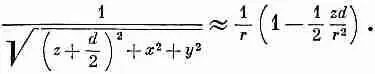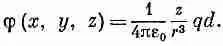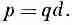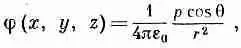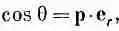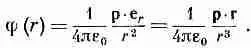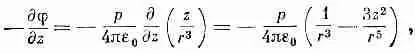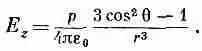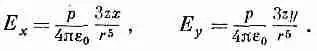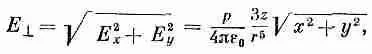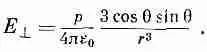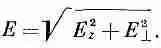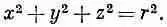
Удобно обозначить

Тогда

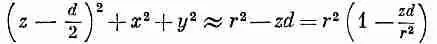
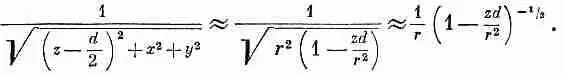
и

Разлагая в биномиальный ряд [1 — (zd/r 2)] -1/2и отбрасывая члены с высшими степенями d , мы получаем

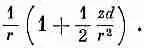
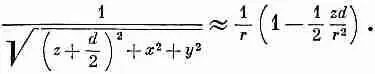
Подобно этому,

Вычитая эти два члена, имеем для потенциала

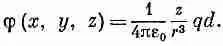
(6.9)

Потенциал, а значит, и поле, являющееся его производной, пропорциональны qd — произведению заряда на расстояния меж­ду зарядами.

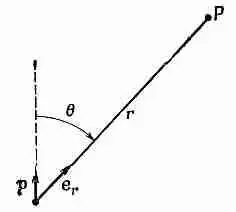
Фиг. 6.3. Векторные обозначения, для диполя.

Это произведение называется диполъным моментом пары зарядов, и мы обозначим его символом р (не путайте с импульсом!):

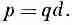
(6.10)

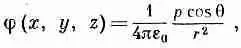
Уравнение (6.9) можно также записать в виде

(6.11)

так как z/r=cosq, где q — угол между осью диполя и радиус-вектором к точке (х, у, z ) (см. фиг. 6.1). Потенциал диполя убы­вает как 1/r 2при фиксированном направлении (а у точечного заряда он убывает как 1/ r ). Электрическое поле Е диполя по­этому убывает как 1/r 3.

Мы можем записать нашу формулу и в векторном виде, если определим р., как вектор, абсолютная величина которого равна р, а направление выбрано вдоль оси диполя от q - к q + . Тогда

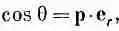
(6.12)

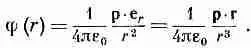
где е r— единичный радиальный вектор (фиг. 6.3). Кроме того, точку (x, y, z) можно обозначить буквой r. Итак, Дипольный потенциал :

(6.13)

Эта формула справедлива для диполя произвольной ориентации и положения, если r — вектор, направленный от диполя к ин­тересующей нас точке.

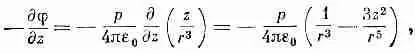
Если нас интересует электрическое поле диполя, то нужно взять градиент j. Например, z-компонента поля есть - d j / dz . Для диполя, ориентированного вдоль оси z , мы можем исполь­зовать (6.9):

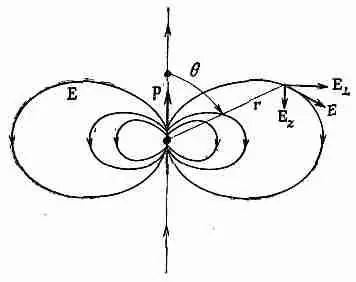
Фиг. 6.4. Электрическое поле диполя.

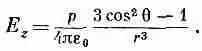
или

(6.14)

А х- и y -компоненты равны

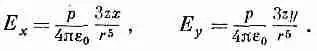
Из этих двух компонент можно составить компоненту, пер­пендикулярную к оси z, которая называется поперечной компонентой E ^:

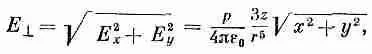
или

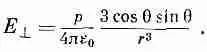
(6.15)

Поперечная компонента Е ^ лежит в плоскости ху и направ­лена прямо от оси диполя. Полное поле, конечно, равно

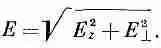
Поле диполя меняется обратно пропорционально кубу рас­стояния от диполя. На оси при 6 =0 оно вдвое сильнее, чем при 9 =90°. При обоих этих углах электрическое поле обладает только z-компонентой. Знаки ее при 2=0 и при z=90° проти­воположны (фиг. 6.4).

§ 3 . Замечания о векторных уравнениях

Здесь, пожалуй, уместно сделать общее замечание, касаю­щееся векторного анализа. Хотя его теоремы и доказаны в общем виде, однако, приступая к расчетам и анализу какой-либо за­дачи, следует с толком выбирать направление осей координат. Вспомните, что когда мы вычисляли потенциал диполя, то ось выбиралась не как попало, а мы направили ее по оси диполя.