Feynmann - Feynmann 5a

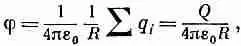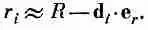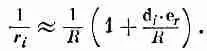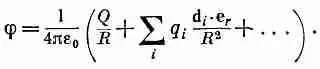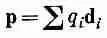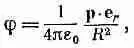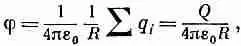
где r i— расстояние от Р до заряда q i (длина вектора R-d i). Если расстояние от зарядов до Р (до точки наблюдения) чрез­вычайно велико, то каждое из r iможно принять за R . Каждый член в сумме станет равным q i / R , и 1 IR можно будет вынести из-под знака суммы. Получится простой результат

(6.22)

где Q — суммарный заряд тела. Таким образом, мы убеди­лись, что из точек, достаточно удаленных от скопления зарядов, оно кажется просто точечным зарядом. Этот результат в общем не очень удивителен.

Но что, если положительных и отрицательных зарядов в группе окажется поровну? Суммарный заряд Q тогда будет равен нулю. Это не такой уж редкий случай; мы знаем, что большинство тел нейтрально. Нейтральна молекула воды, но заряды в ней размещаются отнюдь не в одной точке, так что, приблизившись вплотную, мы должны будем заметить какие-то признаки того, что заряды разделены. Для потенциала произвольного рас­пределения зарядов в нейтральном теле мы нуждаемся в при­ближении, лучшем, чем даваемое формулой (6.22). Уравнение (6.21) по-прежнему годится, но полагать r i = R больше нельзя. Для r iнужно выражение поточнее. В хорошем приближении r iможно считать отличающимся от R (если точка Р сильно уда­лена) на проекцию вектора d на вектор R (см. фиг. 6.7, но вы должны только представлять себе, что Р намного дальше, чем показано). Иными словами, если e r— единичный вектор в нап­равлении R, то за следующее приближение к r i нужно принять

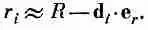
(6.23)

Но нам ведь нужно не r i , а 1/r i; оно в нашем приближении (с учетом d i << R ) равно

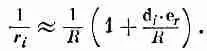
(6.24)

Подставив это в (6.21), мы увидим, что потенциал равен

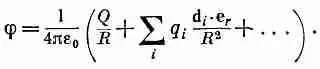
(6.25)

Многоточие указывает члены высшего порядка по d / R , ко­торыми мы пренебрегли. Как и те члены, которые мы выписали, это последующие члены разложения 1/ r i в ряд Тэйлора в ок­рестности 1 / R по степеням d i / R ,

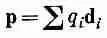
Первый член в (6.25) мы уже получили; в нейтральных телах он пропадает. Второй член, как и у диполя, зависит от 1/R 2. Действительно, если мы определим

(6.26)

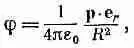
как величину, описывающую распределения зарядов, то вто­рой член потенциала (6.25) обратится в

(6.27)

т. е. как раз в дипольный потенциал. Величина р называется дипольным моментом распределения. Это обобщение нашего прежнего определения; оно сводится к нему в частном случае точечных зарядов.

В итоге мы выяснили, что достаточно далеко от любого набора зарядов потенциал оказывается дипольным, лишь бы этот набор был в целом нейтральным. Он убывает, как 1 / R 2 , и меняется, как cos 0, а величина его зависит от дипольного момента распределения зарядов. Именно по этой причине поля диполей и важны; сами же по себе пары точечных зарядов встре­чаются крайне редко.

У молекулы воды, например, дипольный момент довольно велик. Электрическое поле, создаваемое этим моментом, ответ­ственно за некоторые важные свойства воды. А у многих моле­кул, скажем у СO 2, дипольный момент исчезает благодаря их симметрии. Для таких молекул разложение нужно проводить еще точнее, до следующих членов потенциала, убывающих как 1/R 3и называемых квадрупольным потенциалом. Эти случаи мы рассмотрим позже.

§ 6. Поля заряженных проводников

Мы покончим на этом с примерами таких физических задач, в которых распределение зарядов известно с самого начала. Такие задачи решаются без особых затруднений, в худшем слу­чае требуя нескольких интегрирований. Теперь мы обратимся

к совершенно новому типу задач — определению полей вблизи заряженных проводников.

Представим себе, что какие-то заряды, произвольные по ве­личине Q , помещены на проводнике. Теперь уже мы не можем точно сказать, где они расположатся. Они как-то растекутся по поверхности. Как же узнать, как они на ней распределятся? Распределиться они должны так, чтобы потенциал вдоль всей поверхности был одним и тем же. Если бы поверхность не была эквипотенциальной, то внутри проводника существовало бы электрическое поле и заряды вынуждены были бы двигаться до тех пор, пока поле не исчезло бы. Общую задачу такого рода можно было бы решать так. Предположим, что распределение зарядов такое-то, и рассчитаем потенциал. Если он оказывается на поверхности повсюду одинаковым, то задача решена. Если же поверхность не эквипотенциальна, то значит, мы сделали непра­вильное предположение о распределении зарядов; сделаем но­вое предположение и постараемся, чтобы оно было удачнее! Так может продолжаться без конца, разве что вы здорово набье­те руку на таких пробах.