Feynmann - Feynmann 4a

Нетрудно догадаться, что при этом произой­дет. Действуя так же, как прежде, давайте предположим, что имеются два одинаковых осциллирующих источника с одной и той же частотой, причем фазы их подобраны так, что в некоторую точку Р сигналы приходят с оди­наковой фазой. Если это свет, то в этой точке он очень ярок, если это звук, то он очень громок, а если это электроны, то их очень много. С другой стороны, если приходящие волны отличаются по фазе на 180°, то в точке Р не будет никаких сигналов, ибо полная амплитуда будет иметь здесь минимум. Предположим теперь, что некто крутит ручку «регулировка фазы» одного из источников и меняет разность фаз в точке Р то туда, то сюда, скажем сначала он делает ее нулевой, затем — равной 180° и т. д. При этом, разумеется, будет меняться и сила приходящего сигнала. Ясно теперь, что если фаза одного из источников медленно, постоянно и равномерно меняется по сравнению с другим, начиная с нуля, а затем возрастает постепенно до 10, 20, 30, 40° и т. д., то в точке Р мы увидим ряд слабых и сильных «пульсаций», ибо когда разность фаз проходит через 360°, в амплитуде снова возникает максимум. Но утверждение, что один источник с постоянной скоростью меняет свою фазу по отношению к другому, равносильно утверждению, что число колебаний в 1 сек у этих двух источников несколько различно.

Итак, теперь известен ответ: если взять два источника, ча­стоты которых немного различны, то в результате сложения получаются колебания с медленно пульсирующей интенсив­ностью. Иначе говоря, все сказанное здесь действительно имеет отношение к делу!

Этот результат легко получить и математически. Предположим, например, что у нас есть две волны и забудем на минуту о всех пространственных соотношениях, а просто посмотрим, что приходит в точку Р. Пусть от одного источника приходит волна cosw 1t, а от другого — волна cosw 2t, причем обе частоты w 1и w 2не равны в точности друг другу. Разумеется, амплитуды их тоже могут быть различными, но сначала давайте предположим, что амплитуды равны. Общую задачу мы рассмотрим позднее. Полная амплитуда в точке Р при этом будет суммой двух косинусов. Если мы построим график зависимости амплитуды от вре­мени, как это показано на фиг.48.1,то окажется, что, когда гребни двух волн совпадают, получается большое отклонение, когда совпадают гребень и впадина — практически нуль, а когда гребни снова совпадают, вновь получается большая волна.

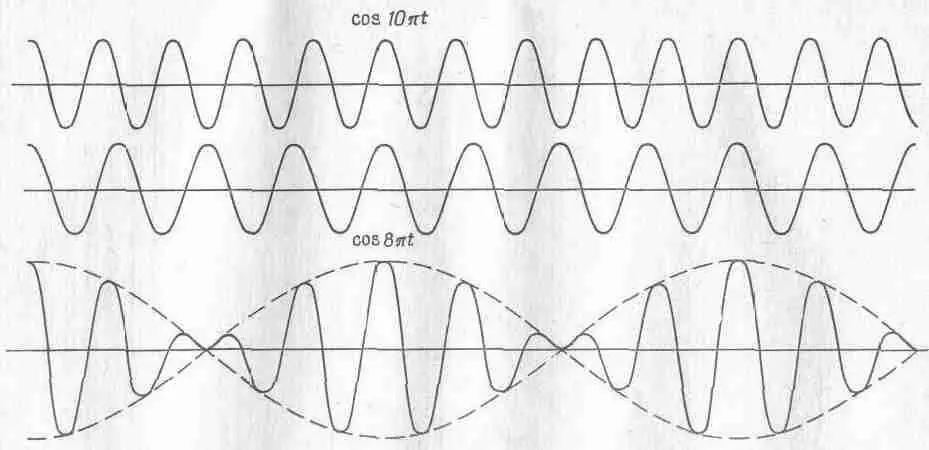
Фиг. 48.1. Суперпозиция двух косинусообразных волн с отношением частот 8:10. Точное повторение колебаний внутри каждого биения для общего случая не типично.

Математически нам нужно взять сумму двух косинусов и как-то ее перестроить. Для этого потребуются некоторые полез­ные соотношения между косинусами. Давайте получим их. Вы знаете, конечно, что

e i ( a + b )=e iae ib (48.1)

и что вещественная часть экспоненты e ia равна cos а, а мни­мая часть равна sin а. Если мы возьмем вещественную часть ехр [-i ( a + b )], то получим cos ( a +b), а для произведения

e ia e ib =(cos a+ i sin a) (cos b+i sin b)

мы получаем cos a cos b - sinasinb плюс некоторая мнимая добавка. Сейчас, однако, нам нужна только вещественная часть. Таким образом,

cos ( a + b ) =cos a cos b - sin a sin b . (48.2)

Если теперь изменить знак величины b , то, поскольку коси­нус при этом не изменяет знака, а синус изменяет знак на обратный, мы получаем аналогичное выражение для косинуса разности

cos (a-b) =cos a cos b+ sin a sin b. (48.3)

После сложения этих двух уравнений произведение синусов сократится, и мы находим, что произведение двух косинусов равно половине косинуса суммы плюс половина косинуса разности

cos a cos b = 1 / 2 cos ( а + b ) + 1 / 2 cos (a-b ). (48.4)

Теперь можно обернуть это выражение и получить формулу для cosa+cosb, если просто положить a = а+b, a b= а- b , т. е. a = 1/ 2(a+b), a b= 1/ 2(a-b):

cosa+cosb=2cos 1/ 2(a+b) cos 1/ 2(a-b). (48.5)

Но вернемся к нашей проблеме. Сумма cosw 1t и cosw 2t равна

cosw 1t+cosw 2t=2cos 1/ 2(w 1+w 2)tcos 1/ 2(w 1-w 2)t. (48.6)

Пусть теперь частоты приблизительно одинаковы, так что 1/ 2(w 1+w 2) равна какой-то средней частоте, которая более или менее та же, что и каждая из них. Но разность w 1-w 2 гораздо меньше, чем w 1и w 2, поскольку мы предположили, что w 1и w 2приблизительно равны друг другу. Это означает, что результат сложения можно истолковать так, как будто есть косинусообразная волна с частотой, более или менее равной пер­воначальным, но что «размах» ее медленно меняется: он пульси­рует с частотой, равной 1 l 2 ( w 1 - w 2 )- Но та ли это частота, с которой мы слышим биения? Уравнение (48.6) говорит, что амплитуда ведет себя как cos 1/ 2(w 1-w 2), и это надо понимать так, что высокочастотные колебания заключены между двумя косинусоидами с противоположными знаками (пунктирная линия на фиг. 48.1). Хотя амплитуда действительно меняется с частотой 1/ 2(w 1-w 2), однако если речь идет об интенсивности волн, то мы должны представлять себе частоту в два раза боль­шую. Иначе говоря, модуляция амплитуды в смысле ее интен­сивности происходит с частотой w 1-w 2, хотя мы и умножаем на косинус половинной частоты.