Feynmann - Feynmann 4a

Это весьма простое соотношение и составляет точное содержа­ние свойства II.

Перейдем теперь к свойству I. Предположим, что положение элемента объема воздуха, не возмущенного звуковой волной, есть х, а звук смещает его в момент времени t на величину c (х, t ), так что его новое положение есть x+c(x,t), как показано на фиг. 47.3.

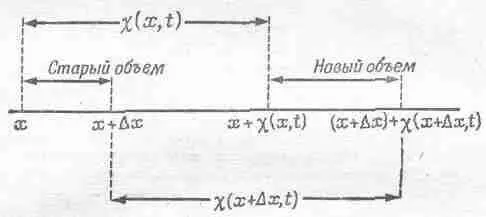
Фиг. 47.3. Смещение воздуха в точке х есть c (х, t ), а в точке х + D х равно c ( x + D x , t ).

Первоначальный объем, приходящийся на единицу площади в плоской звуковой волне, есть D x , а окончательный объем равен D x + c ( x + D x , t ) - c ( x , t ).

Далее, положение соседнего элемента объема есть х + D х, и его смещенное положение есть х + D х + c (х + D х, t ). Теперь можно найти изменение плотности. Поскольку мы рас­сматриваем плоскую волну, удобно взять единичную площадку, перпендикулярную оси х, т. е. направлению распространения волны. Количество воздуха, приходящееся на единичную площадку в интервале D x, есть r 0 D x, где r 0— невозмущенная, или равновесная, плотность воздуха. Эта порция воздуха, сме­щенная звуковой волной, будет находиться теперь между x + c ( x , t ) и x+ D х+ c (х + D х , t ), причем количество воздуха в этом интервале то же самое, что в интервале D x до прихода волны. Если через r обозначить новую плотность, то

r 0 D x = r [ x + D x + c ( x + D x , t )- x - c ( x , t )]. (47.5)

Поскольку D x мало, можно написать c (x+ D x, t )- c (x,t)=( д c /д x ) D x. Здесь уже появляется частная производная, потому что c зависит и от x, и от времени. Наше уравнение принимает вид

r 0 D x =r (( д c / д x) D x + D x), (47.6)

или

r 0=(r 0+r u) д c / д x+r 0+r u. (47.7)

Но в звуковой волне все изменения малы, так что r uмало, c мало и д c /дх тоже мало. Поэтому в уравнении, которое мы только что написали,

r u=-r 0( д c / д x)- r u( д c / д x), (47.8)

можно пренебречь r u (д c /дх) по сравнению с r 0 (д c /дх). Так мы приходим к соотношению, которое требовалось согласно свойству I:

(I) r u=-r 0 д c/ д x. (47.9)

Именно такой вид уравнения можно было ожидать из чисто физических соображений. Если смещение различно для разных х, плотность будет изменяться. Знак тоже правильный: если сме­щение c растет с ростом х, так что воздух расширяется, плотность должна уменьшаться.

Теперь нам нужно найти третье уравнение — уравнение движения, производимого избытком давления. Зная соотноше­ние между силой и давлением, можно получить уравнение дви­жения. Возьмем объем воздуха толщиной Dx и с единичной пло­щадью грани, перпендикулярной х, тогда масса воздуха в этом объеме есть r 0Dx, а ускорение воздуха есть д 2 c / д t 2 , так что масса, умноженная на ускорение для этого слоя, есть r 0Dx( д 2c/ д t 2). (Если Dx; мало, то безразлично, где брать ускорение — на краю слоя или где-нибудь посредине.) Сила, действующая на единич­ную площадку нашего слоя, перпендикулярную оси x, должна быть равна r 0Dx( д 2хc/ д t 2). В точке х мы имеем силу Р(х, t ), дей­ствующую на единицу площади в направлении + х, а в точке x+Dx; возникает сила в обратном направлении, по величине равная Р(x;+ Dx, t ) (фиг. 47.4):

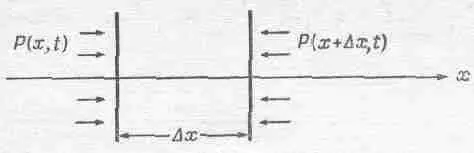
Фиг. 47.4. Результирующая сила в направлении оси х, возникающая за счет давления на единичную площадку, перпендикулярную к оси х, есть — (дР / дх) D х.

Р(х, t )- P ( x + D x , t )=-( д P/ д x) Dx=( д P u/ д x) Dx. (47.10)

Мы учли, что Dx; мало и что только избыточное давление Р и меняется в зависимости от х. Итак, согласно свойству III мы получаем

(III) r 0= д 2c/ д t 2=- д P u/ д x. (47.11)