Feynmann - Feynmann 4a

Глава 46

ХРАПОВИК И СОБАЧКА

§ 1. Как действует храповик

§ 2. Храповик как машина

§ 3. Обратимость в механике

§ 4. Необрати­мость

§ 5. Порядок и энтропия

§ 1. Как действует храповик

В этой главе мы поговорим о храповике и собачке — очень простом устройстве, позволяю­щем оси вращаться только в одном направлении. Возможность получать одностороннее вращение заслуживает глубокого и тщательного анализа, из него проистекут интересные заключения.

Вопросы, которые мы будем обсуждать, воз­никают при попытке найти с молекулярной или кинетической точки зрения простое объяснение тому, что существует предел работы, которая мо­жет быть получена от тепловой машины. Правда, мы уже знаем сущность доказательства Карно, но было бы приятно найти и элементарное его объяснение — такое, которое показало бы, что так физически на самом деле происходит. Суще­ствуют, конечно, сложные, покоящиеся на зако­нах Ньютона математические доказательства ограниченности количества работы, которое можно получить, когда тепло перетекает с од­ного места в другое; но очень непросто сделать эти доказательства элементарными. Короче говоря, мы не понимаем их, хотя можем просле­дить выкладки.

В доказательстве Карно то обстоятельство, что при переходе от одной температуры к дру­гой нельзя извлечь неограниченное количество тепла, следует из другой аксиомы: если все происходит при одной температуре, то тепло не может быть превращено в работу посредством циклического процесса. Поэтому первым делом попытаемся понять, хотя бы на одном элементар­ном примере, почему верно это более простое утверждение.

Попробуем придумать такое устройство, что­бы второй закон термодинамики нарушался, т. е. чтобы работу из теплового резервуара получали, а перепада температур не было. Пусть в сосуде находится газ при некоторой тем­пературе, а внутри имеется вертушка (фиг. 46.1), причем будем считать, что T 1 = T 2 = T .

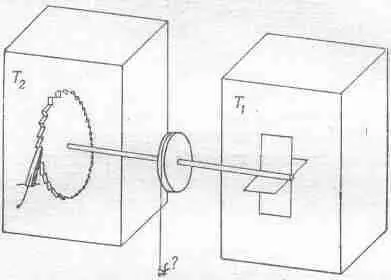
Фиг. 46.1. Машина, состоящая из храповика и собачки.

От ударов молекул газа вертушка будет покачиваться. Нам остается лишь пристроить к другому концу оси колесико, которое может вертеться только в одну сторону,— храповичок с собачкой. Собачка пресечет попытки вертушки поворачиваться в одну сторону, а повороты в другую—разрешит. Колесико будет медленно поворачиваться; может быть, удастся даже подвесить на ниточку блошку, привязать нить к барабану, насаженному на ось, и поднять эту блошку!

Возможно ли это? По гипотезе Карно — нет. Но по первому впечатлению — очень даже возможно (если только мы верно рас­судили). Видно, надо посмотреть повнимательнее. И действи­тельно, если вдумаешься в работу храповика с собачкой, все оказывается не так просто.

Во-первых, хотя наш идеализированный храповик и пре­дельно прост, но есть еще собачка, а при ней положено быть пружинке. Проскочив очередной зубец, собачка должна воз­вратиться в прежнее положение, так что без пружинки не обой­тись.

Весьма существенно и другое свойство храповика и собачки (на рисунке его нельзя показать). Предположим, что части наше­го устройства идеально упруги. Когда собачка пройдет через ко­нец зубца и сработает пружинка, собачка ударится о колесико и начнет подпрыгивать. Если в это время произойдет очередная флуктуация, вертушка может повернуться и в другую сторону, так как зубец может проскользнуть под собачкой, когда та приподнята! Значит, для необратимости вертушки важно, чтобы было устройство, способное гасить прыжки собачки. Но при этом гашении энергия собачки перейдет к храповику и примет вид тепловой энергии. Выходит, что по мере вращения храповик будет все сильнее нагреваться. Для простоты пусть газ вокруг храповика уносит часть тепла. Во всяком случае, вместе с хра­повиком начнет нагреваться и сам газ. И что же, так будет про­должаться вечно? Нет! Собачка и храповик, сами обладая неко­торой температурой Т, подвержены также и броуновскому дви­жению. Это значит, что время от времени собачка случайно поднимается и проходит мимо зубца как раз в тот момент, когда броуновское движение вертушки пытается повернуть ее назад. И чем горячее предмет, тем чаще это бывает.

Вот отчего наш механизм не будет находиться в вечном дви­жении. Иногда от щелчков по крыльям вертушки собачка под­нимается и вертушка поворачивается. Но иногда, когда вертуш­ка стремится повернуть назад, собачка оказывается уже при­поднятой (из-за флуктуации движений этого конца оси) и храповик действительно поворачивает обратно. В итоге—чистый нуль. И совсем нетрудно показать, что, когда температура в обоих сосудах одинакова, в среднем вращения не будет. Будет, конечно, множество поворотов в ту или иную сторону, но чего мы хотим — одностороннего вращения,— тому не бывать.