Feynmann - Feynmann 4

Это дифференциальное уравнение говорит нам, как убывает плотность по мере увеличения высоты.

Мы располагаем теперь дифференциальным уравнением для плотности частиц n , которая меняется с высотой, но ме­няется так, что производная плотности пропорциональна себе самой. Функция, производная которой пропорциональна себе самой,— это экспоненциальная функция и, значит, решение дифференциального уравнения имеет вид

n = n 0 e - mgh / kT . (40.1)

Здесь постоянная интегрирования n 0 — плотность на высоте h = 0 (которую можно задать произвольно); с высотой плот­ность экспоненциально убывает.

Заметим, что если имеется несколько сортов молекул с разными массами, то число их убывает по разным экспонентам. Число более тяжелых молекул убывает с высотой быстрее, чем число легких молекул. Поэтому можно ожидать, что раз кислород тяжелее азота, то по мере подъема вверх относитель­ное содержание азота в атмосфере (смеси азота и кислорода) будет возрастать. В нашей атмосфере, во всяком случае на доступных высотах, этого фактически не происходит, ибо вслед­ствие воздушных возмущений газы вновь перемешиваются.

Ведь это же не изотермическая атмосфера. Тем не менее на больших высотах преобладают очень легкие газы, например водород, так как молекулы легких газов способны забраться на такую высоту, где все остальные экспоненты уже вымрут (фиг. 40.2).

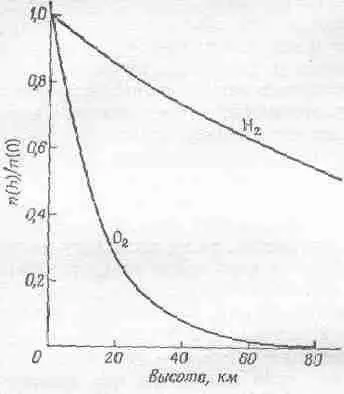
Фиг. 40.2. Нормированная плотность как функция высоты в гравитационном поле Земли для кислорода и водорода при постоян­ной температуре.

§ 2. Закон Болъцмаиа

Отметим здесь тот факт, что числитель показателя экспонен­ты в равенстве (40.1) — это потенциальная энергия, атома. Поэ­тому можно в нашем случае сформулировать закон следующим образом: плотность в каждой точке пропорциональна

e -п.э. / kT

где п.э. — потенциальная энергия отдельного атома.

Возможно, что это случайность и этот закон справедлив только в частном случае однородного гравитационного поля. Однако можно показать, что это весьма общее утверждение. Предположим, что на молекулы газа действуют какие-то иные, не гравитационные, силы. Например, молекулы обладают электрическим зарядом, а тогда они реагируют на электричес­кое поле или на другой заряд, притягивающий их. А может быть, в результате взаимного притяжения атомов друг к другу или к стенкам, или к какому-нибудь твердому телу, или еще к чему-то существуют какие-то силы притяжения, которые зависят от взаимного расположения молекул и действуют на все молекулы. Предположим теперь для простоты, что все молекулы одинаковы и что сила действует на каждую отдельиую молекулу, так что полная сила, действующая на произ­вольно выделяемую часть газа, равна просто произведению числа молекул на силу, действующую на одну молекулу. Дело совсем упростится, если выбрать систему координат так, что сила Fбудет действовать вдоль оси х.

Так же, как и раньше, рассечем газ двумя параллельными плоскостями, промежуток между которыми равен dx . Тогда сила, действующая на каждый атом, умноженная на число ато­мов в 1 см 3 (обобщение прежнего nmg ) и умноженная на dx , должна сбалансировать изменение давления: Fndx = dP = kTdn . Или, придав этому закону другую форму, которая пригодится позднее, запишем:

F =( kTd / dx ) lnn (40.2)

Теперь заметим, что — Fdx — это работа, которую надо совершить для переноса молекулы из х в х + dx , и если сила F произошла из потенциала, т. е. работу можно описывать с помощью потенциальной энергии, то нужную нам величину можно считать изменением потенциальной энергии (п. э.). Отрицательное изменение потенциальной энергии — это про­изведенная работа Fdx , так что d ( lnn ) = - d (п. э .)/ kT , или после интегрирования

n=(постоянная) е -п.э / kT . (40.3)

Таким образом, то, что нам удалось заметить в частном слу­чае, справедливо вообще. (А что если F не происходит из по­тенциала? Тогда (40.2) просто-напросто не имеет решения. В этом случае, после того как какой-нибудь атом опишет замк­нутый путь, вдоль которого полная работа не равна нулю, энер­гия либо прибавится, либо убавится и равновесие никогда не установится. Температурное равновесие невозможно, если внешние силы, действующие на газ, не консервативны.) Урав­нение (40.3) известно под названием закона Болъцмана. Это еще один из принципов статистической механики: вероятность найти молекулу в заданной точке заданной пространственной конфигурации изменяется экспоненциально, причем показа­тель экспоненты состоит из потенциальной энергии в заданной пространственной конфигурации, взятой с обратным знаком и деленной на kT .