Feynmann - Feynmann 1

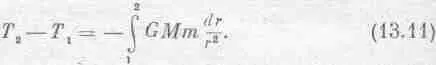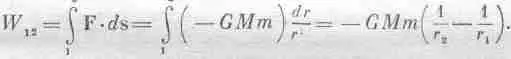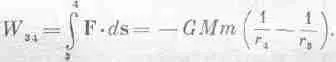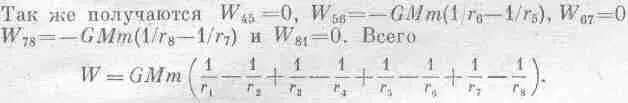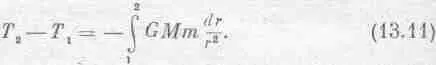
Этот одномерный случай рассматривать легко, потому что мы знаем, что изменение кинетической энергии равно интегралу от начала движения до конца от силы — GMm / r 2 по перемеще­нию dr

В формуле нет никакого косинуса, потому что сила и перемеще­ние направлены одинаково. Интегрировать dr / r 2 легко; получает­ся (—1/г), так что

Перед нами другая формула для потенциальной энергии. Уравнение (13.12) говорит нам, что величина 1/ 2 mv 2 - GMm / r , вычисленная в точке 1, в точке 2 или в любой другой, остается постоянной.

У нас теперь есть формула для потенциальной энергии в поле тяготения для вертикального движения. Здесь возникает интересный вопрос: можно ли добиться вечного движения в поле тяготения? Поле-то меняется, в разных местах у него разная напряженность и разное направление. Нельзя ли взять беско­нечную ленту без трения и запустить ее, скажем, так: пусть она сперва поднимает тело из одной точки в другую, потом проводит его по дуге окружности в третью точку, опускает на неко­торый уровень, сдвигает по наклонному направлению и выводит на новый путь и т. п., так что по возвращении в началь­ную точку оказывается, что поле тяготения совершило неко­торую работу и кинетическая энергия тела возросла? Нельзя ли так начертить эту траекторию, чтобы, обойдя по ней, тело приобрело чуть-чуть больше скорости, чем имело вначале? Так получится вечное движение. Но ведь оно невозможно, значит, мы обязаны доказать, что такая траектория немыслима.

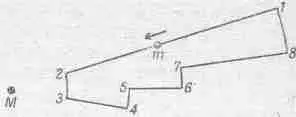
Фиг. 13.3. Замкнутый путь обхода в поле тяготения.

Мы должны доказать следующее предположение: раз трения нет, тело должно вернуться ни с меньшей, ни с большей скоростью, а как раз с такой, чтобы еще и еще делать круги по этому замк­нутому пути. Или, другими словами, вся работа, произведенная в движении по замкнутому пути, должна быть нулем для сил тяжести, потому что если бы она не была нулем, то можно было бы получить энергию за счет такого движения тела. (Если бы работа оказалась меньше нуля, так что скорость в конце обхода уменьшилась бы, то для получения энергии стоило бы только повернуть обратно; силы ведь зависят не от направления дви­жения, а только от положения. Если в одном направлении рабо­та получится с плюсом, то в обратном она будет с минусом; лю­бая ненулевая работа означает создание вечного двигателя.) Так что же, действительно ли работа равна нулю? Попробуем показать, что да. Сперва мы лишь на пальцах поясним, почему это так, а уж потом оформим математически. Положим, мы вы­думали траекторию, показанную на фиг. 13.3; масса падает от 1 к 2, поворачивает до 3, обратно поднимается к 4, затем через 5, 6, 7, 8 движется обратно к 1. Все линии идут либо по радиусу, либо по кругу с центром М. Какая работа совершается на таком пути? Между 1 и 2 она равна произведению GMm

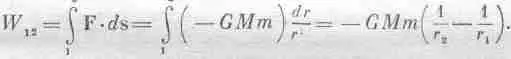
на разность 1/r в этих точках:

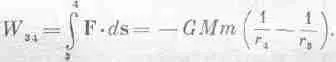
От 2 до З сила в точности направлена поперек движения, и W 23=0. От 3 к 4

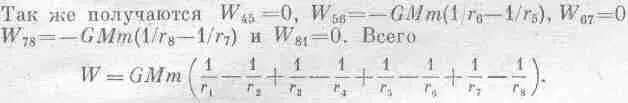
Но ведь r 2=r 3, r 4=r 5, r 6=r 7, r 8 = r 1 . Поэтому W=0.

Но возникает подозрение, не слишком ли эта кривая проста. А что даст настоящая траектория? Что ж, попробуем настоящую. Сразу же ясно, что ее можно достаточно точно пред­ставить как ряд зазубрин (фиг. 13.4) и поэтому... и т. д., что и требовалось доказать.

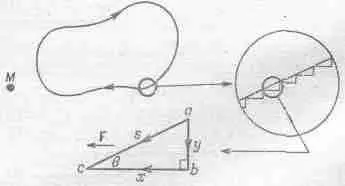
Фиг. 13.4. «Плавный» путь об­хода.

Показан увеличенный отрезок этого пути и близкая к нему траектория, состоящая из радиальных и круговых участков, а также один из зубцов этой траектории.