Feynmann - Feynmann 1

§ 6. Ядерные силы

Мы заключим эту главу кратким обзором единственных ныне известных сил, отличающихся от перечисленных,— ядерных сил. Эти силы действуют внутри ядра атома, и, хотя их много изучали, никто ни разу еще не смог рассчитать силу, действую­щую между двумя ядрами; и фактически закон ядерных сил сей­час не известен. Эти силы имеют крайне незначительную протя­женность действия — они действуют только на размерах ядра около 10 -1 3см. Поскольку частицы столь малы, а расстояния так коротки, нам нечего надеяться на законы Ньютона — здесь действуют только законы квантовой механики. Анализи­руя ядра, мы больше не говорим о силах; мы заменяем понятие силы понятием энергии взаимодействия двух частиц (позже об этом будет сказано подробнее). Любые формулы, которые можно написать для ядерных сил, представляют довольно грубые приближения, в которых опущены многие детали взаимодействия; выглядят они примерно так: силы внутри ядер убывают не обратно квадрату расстояния, а отми­рают экспоненциально за некоторым расстоянием r 0 (порядка 10 -1 3 см) как F =( l / r 2 ) exp (-r/r 0). Иначе говоря, чуть частицы удалятся, как силы тут же исчезают, хотя ближе 10 -1 3 см они очень велики. По-видимому, законы ядерных сил сложны до чрезвычайности; мы их не понимаем, и вся задача анализа фун­даментального механизма, стоящего за ними, не решена. Попыт­ки решить эту задачу привели к открытию множества необыч­ных частиц, например p-мезонов, но происхождение сил все равно остается темным.

Глава 13

РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ( I )

§ 1. Работа падаю­щего тела

§ 2. Работа, выполняемая тяжестью

§ 3, Сложение энергий

§ 4. Поле тяготения больших тел

§ 1. Работа падающего тела

В гл. 4 мы разобрали вопрос о сохранении энергии. При этом законами Ньютона мы не пользовались. Интересно теперь посмотреть, как возникает сохранение энергии из-за того, что действуют эти законы. Для ясности мы начнем с самых простых примеров и постепенно будем их усложнять.

Простейший пример сохранения энергии — это тело, падающее вниз, т. е. тело, движущееся только в вертикальном направлении. Если оно меняет свою высоту под влиянием только тяже­сти, то из-за движения оно обладает кинети­ческой энергией Т (или к. э.) Кроме того, у него есть потенциальная энергия mgh (сокра­щенно U , или п. э.). Их сумма постоянна:

или

Т + U =const. (13.1)

Мы хотим показать, что это утверждение пра­вильно. Что значит доказать его правильность? Второй закон Ньютона говорит, как движется тело, как со временем изменяется его скорость (а именно, что в падении она растет пропорци­онально времени, а высота падения меняется как квадрат времени). Если поэтому отмерять высоту от нулевой точки (где тело покоилось), то не будет ничего странного в том, что она окажется равной квадрату скорости, умножен­ному на какие-то постоянные. Однако все же рассмотрим это повнимательней.

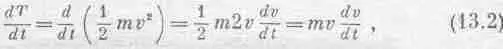
Попробуем вычислить прямо из второго закона Ньютона, как обязана меняться кинетическая энергия; мы продифференцируем кинетическую энергию по времени и потом применим за­кон Ньютона. Дифференцируя 1/ 2 mv 2 по времени, получаем

потому что m считается постоянной. Но по второму закону Ньютона m ( dv / dt )= F , так что

dT / dt = Fv . (13.3)

В общем случае получается F· v, но для нашего одномерного случая лучше оставить просто произведение силы на скорость.

Сила в нашем простом примере постоянна, равна — mg и направлена вниз (знак минус именно это и показывает), а ско­рость есть степень изменения положения по вертикали (высоты h ) со временем. Поэтому степень изменения кинетической энер­гии равна — mg ( dh / dt ). Взгляните: что за чудо! Перед нами снова чья-то скорость изменения — скорость изменения со вре­менем величины mgh ! Поэтому выходит, что с течением времени изменения в кинетической энергии и в величине mgh остаются равными и противоположными, так что их сумма остается не­изменной. Что и требовалось доказать.