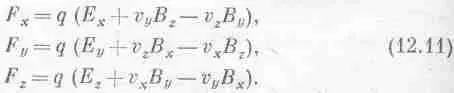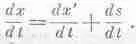Feynmann - Feynmann 1

Во второй части опыта напряжение на пластины уже не подается, а вместо этого проверяется влияние магнитного поля на электронный пучок. Для этого необходим подковообразный магнит, достаточно широкий, чтобы «оседлать» практически всю трубку. Предположим, что мы подвели магнит снизу к трубке, обхватили им ее и направили полюсы кверху (в виде буквы U). Мы замечаем, что пятно на экране смещается, скажем кверху, когда магнит приближается снизу. Выходит, что магнит отталкивает пучок. Но не так все просто: если мы пере­вернем магнит, не переставляя его сторон, и приблизим его к трубке сверху, то пятно снова сдвинется вверх, т. е. вместо оттал­кивания наступило притяжение. А теперь вернем магнит в пер­воначальное положение, когда он обхватывал трубку снизу. Да, пятно по-прежнему отклоняется кверху; но повернем маг­нит на 180° вокруг вертикальной оси, чтобы он имел вид буквы U, но уже с переставленными полюсами. Смотрите-ка, пятно прыгает вниз и остается там, даже если мы переворачиваем те­перь U вверх ногами.

Чтобы понять такое своеобразное поведение, нужно приду­мать какую-то иную комбинацию сил. Объясняется все это вот как. Вдоль магнита, от полюса к полюсу, тянется магнитное поле. Оно направлено всегда от одного определенного полюса (который можно снабдить какой-нибудь меткой) к другому. Вращение магнита вокруг его оси не меняет направления поля, а перестановка полюсов местами меняет. Например, если электроны летят горизонтально по оси х, а магнитное поле тоже горизонтально, но направлено по оси у, то магнитная сила, действующая на движущийся электрон, направлена по оси z (вверх или вниз, это уже зависит от того, как направлено поле — по оси у или против нее).

Мы пока не дадим полного закона сил взаимодействия заря­дов, движущихся друг относительно друга в произвольных на­правлениях, потому что он чересчур сложен, но зато приведем формулы для случая, когда поля известны. Действие силы на заряженный предмет зависит от его движения; когда предмет неподвижен, сила, действующая на него, считается пропорцио­нальной заряду с коэффициентом, называемым электрическим полем. Когда тело движется, сила изменяется, и поправка, но­вый «кусок» силы, оказывается линейно зависящей от скорости и направленной поперек скорости v и поперек другой вектор­ной величины — магнитной индукции В. Когда составляющие электрического поля Еи магнитной индукции В суть соответ­ственно (Е х , Е у , Е г ,) и (В х , B y , B z ), a составляющие скорости v суть ( v x , v y , v z ), то составляющие суммарной электрической и магнитной сил, действующих на движущийся заряд q , таковы:

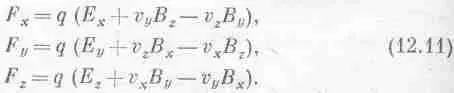
Если случайно магнитное поле имеет только компоненту B y , а скорость — только v x , то у магнитной силы остается состав­ляющая вдоль z, поперек В и у.

§5 Псевдосилы

Очередной тип сил, который нам предстоит рассмотреть,— это псевдосилы.

В гл. 11 мы обсудили взаимоотношение двух молодых людей, Джо и Мика, обладателей различных систем координат. Пусть положение частицы по измерениям Мика есть x , а Джо дает для нее х'; тогда связь между ними такова:

x=x'+s, y=y' z=z',

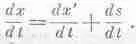
где s показывает, насколько сместилась система Джо отно­сительно системы Мика. Пусть у Мика в системе выполняются законы движения. Как они выглядят для Джо? Сперва мы обна­ружим, что

Раньше мы считали s постоянной и убедились, что законы дви­жения при этом не меняются, так как ds / dt =0; в конечном сче­те в обеих системах все законы физики одинаковы. Но пусть s = ut , где u — постоянная скорость движения по прямой. Тогда s непостоянна и ds / dt — не нуль, а u, т. е. константа. Но ускоре­ние d 2 x / dt 2 такое же, как d 2 x '/ dt 2 , потому что du / dt =0 . Этим до­казывается закон, использованный в гл. 10, а именно: когда мы движемся по прямой с постоянной скоростью, все законы фи­зики выглядят так, как если бы мы стояли. Это преобразова­ние Галилея. А теперь мы хотим рассмотреть случай поинтерес­нее, когда s зависит от времени еще сложнее, например s = at 2 /2. Тогда ds / dt = at , а d 2 s / dt 2 = a , т . е. ускорение по­стоянно; можно рассмотреть также случай, когда ускорение само оказывается функцией времени. Это значит, что хотя закон силы с точки зрения Джо выглядит как