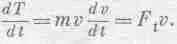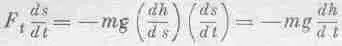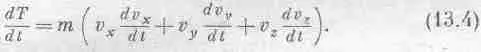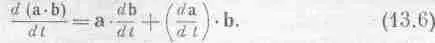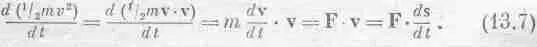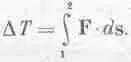Feynmann - Feynmann 1

Мы только что показали, пользуясь Вторым законом Нью­тона, что для постоянных сил энергия сохраняется, если только прибавлять потенциальную энергию mgh к кинетической 1 / 2 mv 2 . Исследуем этот вопрос дальше; посмотрим, можно ли его обобщить, можно ли еще продвинуться в его понимании. Действует ли этот закон только для свободно падающих тел или является более общим? Из того, что мы знаем о сохранении энергии, можно ожидать, что он будет верен для тела, движу­щегося из одной точки в другую по кривой без трения и под дей­ствием одной лишь тяжести (фиг. 13.1). Когда тело, начав дви­гаться с высоты Н, достигает высоты h , то опять должна быть верной та же формула, хотя бы скорость уже не была направле­на по вертикали. Нам надо понять, почему она все еще правильна. Проведем тот же анализ; отыщем скорость изменения кинетиче­ской энергии во времени. Опять будет получаться mv ( dv / dt ) — скорость изменения величины импульса, т. е. сила в направлении движения — касательная сила F t . Итак,

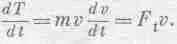
Скорость—это скорость изменения расстояния вдоль кривой ds / dt , а касательная сила F t теперь оказывается меньше mg в отношении, равном отношению расстояния ds вдоль пути к вер­тикальному расстоянию dh . Иными словами,

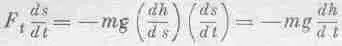
так что

( ds выпадает). И опять, как прежде, мы получили величину — mg ( dh / dt ), равную скорости изменения mgh .

Чтобы точно уяснить себе, как вообще соблюдается сохра­нение энергии в механике, рассмотрим сейчас некоторые полез­ные понятия.

Во-первых, рассмотрим скорость изменения кинетической энергий в общем трехмерном случае. Кинетическая энергия, когда движение имеет три измерения, равна

T =1/2 m ( v 2 x + v 2 y + v 2 z ).

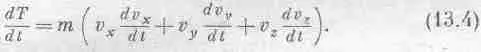
Дифференцируя ее по времени, получаем три устрашающих члена:

Но ведь m ( dv x / dt ) — это сила F x , действующая на тело в на­правлении х. Значит, в правой части формулы (13.4) стоит F x v x + F y v y + F z v z . Призвав на помощь векторный анализ, вспоминаем, что это F· v .Итак,

dT/dt= F· v (13.5)

А можно это вывести и быстрей: если аи b— два вектора, зави­сящих от времени, то производная от a· bравна

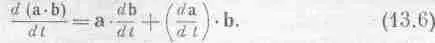
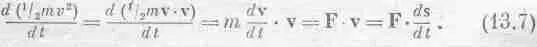
Подставим сюда а= b = v :

Так как понятие кинетической энергии и вообще энергии очень важно, то различным величинам в этих уравнениях при­своены разные имена: l / z mv 2 называется, как известно, кинети­ческой энергией; F· vназывается мощностью: сила, действующая на тело, умноженная («скалярно») на скорость тела,— это мощность, сообщаемая телу этой силой. Получается великолеп­ная теорема: скорость изменения кинетической энергии тела рав­на мощности, затраченной силами, действующими на тело. Но для изучения сохранения энергии анализ следует продол­жить. Давайте оценим изменение кинетической энергии за очень короткое время dt . Умножив обе части уравнения (13.7) на dt , найдем, что изменение кинетической энергии равно силе, скалярно умноженной на дифференциал пройденного расстояния

dT = F · ds . (13.8)

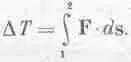
А интегрируя, получаем

(13.9)