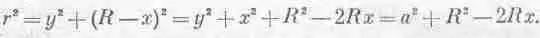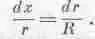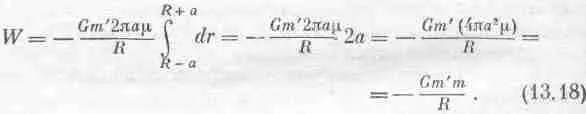Feynmann - Feynmann 1

то работа равна

Стало быть, вся работа равна сумме работ, произведенных про­тив силы 1 и против силы 2, как если бы они действовали неза­висимо. Продолжая рассуждать таким образом, мы увидим, что полная работа, которую необходимо выполнить, чтобы собрать данную конфигурацию тел, в точности равна значению (13.14) для потенциальной энергии. Именно из-за того, что тяготение подчиняется принципу наложения сил, можно потенциальную энергию представить в виде суммы по всем парам частиц.

§ 4. Поле тяготения больших тел

Теперь рассчитаем поля, встречающиеся во многих физиче­ских задачах, когда речь идет о распределении масс. Мы пока не рассматривали распределения масс, а занимались только отдель­ными частицами. Но интересно рассчитать и поля, образуемые более чем одной частицей. Для начала найдем силу притяжения со стороны плоского пласта вещества бесконечной протяженности. Сила притяжения единичной массы в данной точке Р (фиг. 13.5), конечно, направлена к плоскости. Расстояние от точки до пло­скости есть a, а масса единицы площади этой плоскости есть m., где m=m/4pa 2— поверхностная плотность массы. (Вообще пло­щадь поверхности шарового пояса пропорциональна его вы­соте.) Поэтому потенциальная энергия притяжения массы dm есть

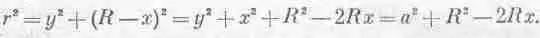
Но мы видим, что

Значит,

2 rdr =-2 Rdx ,

или

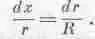
Поэтому

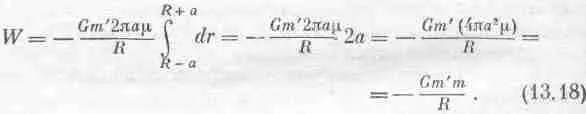
и получается

Стало быть, для тонкого слоя потенциальная энергия массы m ', внешней по отношению к слою, такова, как если бы масса слоя собралась в его центре. Землю же можно представить в виде ряда таких слоев, и притяжение каждого из слоев зависит только от его массы; сложив их, получим всю массу планеты; значит, и вся Земля действует так, словно все ее вещество находится в ее центре!

Но посмотрим, что произойдет, если точка Р окажется внутри слоя. Проделывая те же расчеты вплоть до интегрирования, мы получим разность двух значений r, но уже в другой форме: ( a + R )- (а - R )=2 R (двойное расстояние от Р до центра). Дру­гими словами, теперь W становится равной W =- Gmm '/ a , что не зависит от R , т. е. точка Р всюду внутри сферы обладает одной и той же энергией тяготения. А значит, на нее не дей­ствует никакая сила, и не нужно никакой работы, чтобы двигать ее внутри. Когда потенциальная энергия тела всюду, в любой точке внутри сферы, одинакова, то на тело не действует никакая сила. Внутри сферы тело не испытывает действия сил, сила действует только снаружи.

* Энергия в единицах табл. 9.2 есть Ѕ ( v 2 x + v 2 y )-1/ r

Глав а 14

РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ( II )

§1. Работа

§2. Движение при наложенных связях

§3. Консерватив­ные силы

§4. Неконсерватив­ные силы

§5. Потенциалы и поля

§ 1. Работа

В предыдущей главе мы ввели много новых понятий и идей, играющих важную роль в физике. Идеи эти столь важны, что, пожалуй, стоит посвятить целую главу внимательному ознакомлению с ними. Мы не будем здесь повторять «доказательства» и красивые приемы, поз­воляющие просто получать важные результаты, а вместо этого сосредоточим наше внимание на обсуждении самих идей.

Штудируя любой вопрос технического харак­тера, для понимания которого нужна математика, мы всегда сталкиваемся с необходимо­стью понять и отложить в памяти массу фактов и идей, объединенных определенными связями, Существование этих связей можно «доказать или «показать». Ничего не стоит спутать само доказательство с тем соотношением, которое оно устанавливает. Конечно, куда важнее вы­учить и запомнить не доказательство, а само соотношение. Тогда уж в любом случае мы смо­жем сказать: «Легко показать, что...» то-то и то-то верно, а то и действительно показать это, Приводимые доказательства почти всегда со­стряпаны, сфабрикованы с таким расчетом чтобы, во-первых, их легко было воспроизвести мелом на доске или пером на бумаге и, во-вто­рых, чтобы они выглядели поглаже. В итоге доказательство выглядит обманчиво просто, хотя, быть может, на самом деле автор много часов искал разные пути расчета, пока не нашел самый изящный — тот, который приводит к ре­зультату за кратчайшее время! Глядя на вывод формулы, надо вспоминать не этот вывод, а скорее сам факт, что то-то и то-то можно доказать. Конечно, если доказательство требует особых математических выкладок или «трюков», никогда прежде не виденных, то надо обратить внимание... впрочем, не на сами трюки, а на их идею.