Нихиль Будума - Основы глубокого обучения

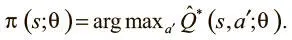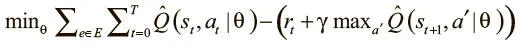
Она полностью дифференцируема как функция параметров нашей модели, и можно найти для нее градиенты для использования в стохастическом градиентном спуске и минимизации потерь.

Вы наверняка уже заметили проблему: мы определяем функцию потерь на основе разницы предсказанного Q-значения нашей модели для этого шага и для следующего. Получается, потери вдвойне зависят от параметров модели.

При каждом обновлении параметров Q-значения сдвигаются, а мы используем их для дальнейших обновлений. Высокая корреляция обновлений может привести к циклам обратной связи и нестабильности в обучении, поскольку параметры порой значительно колеблются и функция потерь не сходится.

Чтобы устранить эту проблему корреляции, можно использовать пару простых инженерных хитростей: это целевая Q-сеть и воспроизведение опыта.

Вместо постоянного обновления одной сети по отношению к самой себе можно снизить взаимозависимость, введя вторую, которая называется целевой. Наша функция потерь относится к случаям Q-функци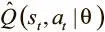и, и .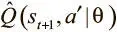

Мы представим первое Q как предсказательную сеть, а второе будет выдаваться целевой Q-сетью. Последняя — копия предсказательной сети с задержкой обновления параметров.

Мы обновляем целевую Q-сеть в соответствии с предсказательной только через каждые несколько пакетов. Это дает необходимую стабильность Q-значениям, и теперь можно должным образом изучить хорошую Q-функцию.

Есть еще один источник досадной нестабильности в обучении: высокие корреляции последних действий. Если обучать DQN на пакетах из недавнего опыта, все пары (состояние, действие) будут взаимосвязаны. Это вредно, поскольку мы хотим, чтобы градиенты пакета представляли весь градиент; а если данные нерепрезентативны для распределения данных, пакетный градиент не будет точным приближением истинного.

Поэтому нам нужно разбить корреляцию данных в пакетах. Это можно осуществить при помощи повторения опыта . Мы сохраняем весь опыт агента в таблице, а чтобы создать пакет, проводим случайную выборку. Опыт хранится в таблице в виде кортежей ( s i, a i, r i, s i + 1). Из этих четырех значений можно вычислить функцию потерь, а с ней и градиент для оптимизации сети.

Таблица воспроизведения опыта больше похожа на очередь. Опыт, который агент получил на ранних стадиях обучения, может не отражать тот, с которым сталкивается уже обученный агент, так что полезно время от времени удалять очень старый опыт из таблицы.

Q-обучение — парадигма обучения ценностям, а не алгоритм освоения стратегии. Мы не обучаем прямо стратегию действия в среде. А можем ли мы разработать ее на основе данных Q-функции? Если мы нашли хорошую аппроксимацию, мы знаем ценность каждого действия для каждого состояния. И теперь можно тривиально выработать оптимальную стратегию: просмотреть Q-функцию на предмет всех действий в текущем состоянии, выбрать действие с максимальным значением Q, перейти в новое состояние и повторить то же. Если Q-функция оптимальна, выработанная на ее основе стратегия тоже будет оптимальной. И тогда мы можем выразить оптимальную стратегию так:

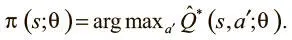
Можно также прибегнуть к техникам семплирования, о которых мы говорили выше, для выработки стохастической стратегии, которая порой отклоняется от рекомендаций Q-функции для варьирования соотношения исследования и использования.

DQN — тоже марковский процесс принятия решений, который опирается на марковское предположение , что следующее состояние s_i + 1 зависит только от текущего s_i и действия a_i, а не от какого-либо предыдущего состояния или действия. Это несправедливо во многих средах, где состояние игры не может быть отражено в едином кадре. Например, в пинг-понге скорость шарика (важный фактор успеха) не может быть получена по одному кадру. 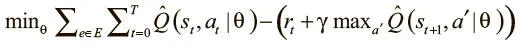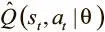Марковское предположение делает моделирование принятия решений гораздо проще и надежнее, но часто ценой мощности модели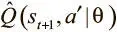.