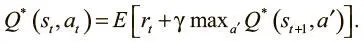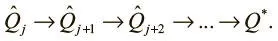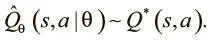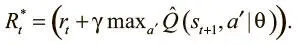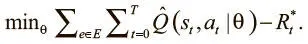Нихиль Будума - Основы глубокого обучения

Мы решаем эту дилемму, определяя значения Q как функцию от будущих значений Q. Такие отношения называются уравнением Беллмана, которое утверждает, что максимальная будущая выгода от действия a — текущая выгода плюс максимальная будущая на следующем шаге от совершения следующего действия a':

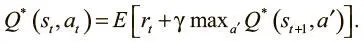
Это рекурсивное определение позволяет установить соответствие между значениями Q в прошлом и будущем, и уравнение удобно задает правило обновления. Мы можем обновить предыдущие значения Q так, чтобы они основывались на будущих. И здесь очень удачно, что мы точно знаем одно верное значение Q: это Q для самого последнего действия перед окончанием эпизода.

Для этого состояния мы точно знаем, что следующее действие привело к новому вознаграждению, и можем точно задать значения Q. Теперь можно использовать правило обновления для распространения этого значения на предыдущий шаг:

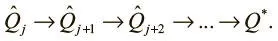
Такое обновление называется итерацией по значениям .

Первое значение Q оказывается неверным, но это приемлемо. С каждой итерацией мы можем обновлять его при помощи верного значения в будущем. После одной итерации последнее значение Q верно, ведь это вознаграждение с последнего состояния и действия перед окончанием эпизода. Затем мы проводим обновление Q и устанавливаем тем самым его значение для второй с конца пары (состояние, действие). На следующей итерации мы можем гарантировать, что верны два последних значения Q, и т. д. Благодаря итерации по значениям гарантируется схождение к конечному оптимальному значению Q.

Итерация по ценностям устанавливает связь между парами состояний и действий и значениями Q, и мы создаем таблицу этих связей, которая называется Q-таблицей .

Коротко поговорим о ее размере. Итерация по ценностям — утомительный процесс, который требует полного обхода всех пар (состояние, действие). Например, в игре Breakout 100 кирпичиков могут либо присутствовать, либо нет, а также есть 50 возможных положений ударной лопатки, 250 возможных позиций шарика и три действия — и уже здесь такой объем, который во много раз превосходит сумму всех вычислительных возможностей человечества. А в стохастических средах объем Q-таблицы будет еще больше — возможно, даже бесконечным. И тогда найти Q-значения всех пар (действие, состояние) станет невозможно. Этот подход явно не сработает. Как же тогда заниматься Q-обучением?

Размер Q-таблицы делает наивный подход неосуществимым для любой реальной задачи. Но что если ослабить требования к оптимальной Q-функции? Если обучать аппроксимацию Q-функции, можно использовать модель для ее оценки.

Вместо того чтобы пытаться исследовать каждую пару (состояние, действие) ради обновления Q-таблицы, можно обучить функцию, которая будет аппроксимировать ее и даже строить обобщения за пределами своего опыта. И нам не придется вести утомительный поиск по всем возможным Q-значениям для обучения функции.

Этим руководствовались в DeepMind при работе над глубокой Q-сетью (Deep Q-Network, DQN). DQN берет глубокую нейронную сеть, которая на основе полученного изображения (состояния) оценивает Q-значение для всех возможных действий.

Мы хотим обучить сеть аппроксимировать Q-функции. Выразим ее аппроксимацию как функцию параметров нашей модели:

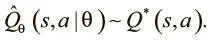
Помните, что Q-обучение — это обучение ценности. Мы осваиваем не саму стратегию, а ценность каждой пары (действие, состояние), независимо от их качества. Аппроксимацию Q-функции нашей модели мы выразили как Qtheta, и мы хотели бы, чтобы она была близка к ожидаемому вознаграждению. Используя уравнение Беллмана, рассмотренное выше, мы можем выразить его так:

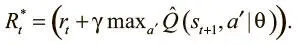
Наша цель — минимизировать разницу между аппроксимацией Q и следующим значением Q:

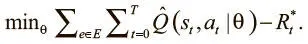
Раскрытие этого выражения дает нам полную целевую функцию: