Нихиль Будума - Основы глубокого обучения

Обучение с подкреплением сейчас интересно многим причастным к работе над искусственным интеллектом, поскольку это общая структура создания разумных агентов. Агент учится взаимодействовать со средой, чтобы увеличить общее вознаграждение. Это лучше соответствует модели развития человека. Да, мы можем построить очень хорошую и точную модель классификации изображений кошек и собак, обучив ее на тысячах рисунков. Но такой подход не используется в начальных школах. Люди взаимодействуют со средой, усваивая представления о мире, на основе которых смогут позже принимать решения. Практическое применение обучения с подкреплением обнаруживаются во многих передовых технологиях: автомобилях без водителя, роботизированном управлении двигателем, играх, контроле кондиционирования воздуха, оптимизации рекламы и стратегиях торговли на фондовом рынке.

В качестве иллюстрации рассмотрим простой пример для решения проблемы управления — балансировку шеста. В задаче есть тележка с шестом, который прикреплен к нему на шарнире и может раскачиваться. Есть также агент, который управляет тележкой, — двигает ее влево или вправо. Есть среда, которая вознаграждает агента, если шест направлен вверх, и штрафует, если тот падает вниз (рис. 9.3).

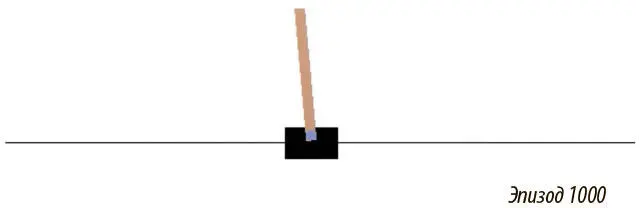
Рис. 9.3. Простой агент обучения с подкреплением, балансирующий шест. Изображение из агента OpenAI Gym Policy Gradient, который будет создан в этой главе

В нашем примере с балансировкой шеста есть несколько важных элементов, которые можно формализовать как марковские процессы принятия решений (MDP). Вот они.

Состояние

У тележки есть ряд возможных положений на оси х . У шеста — ряд возможных углов.

Действие

Агент может совершить действие — сдвинуть тележку влево или вправо.

Переход состояний

Когда агент действует, среда меняется: тележка двигается, шест изменяет угол и скорость.

Вознаграждение

Если агент хорошо балансирует шест, он получает позитивное вознаграждение. Если шест падает, следует негативное подкрепление.

MDP определяется следующим:

• S , конечное множество возможных состояний;

• A , конечное множество действий;

• P ( r, s ′| s, a ), функция перехода между состояниями;

• R , функция вознаграждения.

MDP дают математическую структуру для моделирования принятия решений в заданной среде (рис. 9.4).

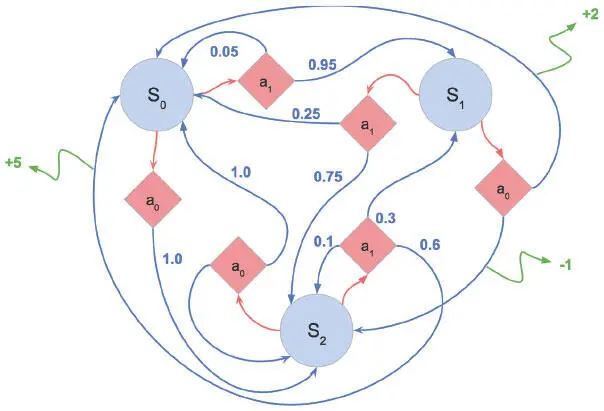
Рис. 9.4. Пример марковского процесса принятия решений. Голубые кружки обозначают состояния среды. Красные ромбы соответствуют возможным действиям. Стрелки от ромбов к кругам отображают переход из одного состояния в другое. Числа при них соответствуют вероятности действия. Числа в конце зеленых стрелок показывают вознаграждение, которое выдается агенту за выполнение соответствующего перехода

Когда агент совершает действие в структуре MDP, образуется эпизод . Он состоит из серии кортежей состояний, действий и вознаграждений. Эпизоды сменяются, пока среда не достигает конечного состояния: например, экрана Game Over в играх Atari или падения шеста в примере с тележкой и шестом. Следующее уравнение показывает все переменные эпизода:

( s 0, a 0, r 0), ( s 1, a 1, r 1), … ( s n, a n, r n ).

В примере с тележкой (cart) и шестом (pole) состояние среды может быть кортежем из положения тележки и угла шеста, например: ( x cart , θ pole ).

Цель MDP — найти оптимальную стратегию для агента. Стратегия — способ действия в зависимости от текущего состояния. Формально ее можно представить в виде функции π , которая выбирает действие a , выполняемое агентом в состоянии s . Цель MDP — найти стратегию максимального увеличения ожидаемой будущей выгоды: max πE[R 0 + R 1 +…R t|π]. Здесь R отражает будущую выгоду от каждого эпизода. А теперь дадим ее более строгое определение.

Будущая выгода — ожидаемые вознаграждения. Выбор оптимального действия требует учитывать не только непосредственные результаты, но и долгосрочные последствия. Например, агент-альпинист, получающий вознаграждения за достижение высоты, может решить немного спуститься, чтобы перейти на более удобный путь к вершине горы.