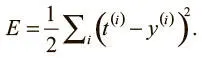Нихиль Будума - Основы глубокого обучения

Мы хотим обучить один линейный нейрон решать эту задачу. Как?

Один из вариантов — разумно подбирать примеры для обучения. Для одного обеда купим один бургер, для второго — одну порцию картошки, для третьего — один стакан газировки. В целом разумный подбор примеров — хорошая идея. Многие исследования показывают, что, создав хорошую подборку данных для обучения, вы сможете заметно повысить эффективность нейросети. Но проблема использования только этого подхода в том, что в реальных ситуациях он редко приближает нас к решению. Например, при распознавании изображений аналога ему нет и решения мы не найдем.

Нам нужно найти вариант, который поможет решать задачу в общем случае. Допустим, у нас очень большой набор обучающих примеров. Это позволит нам вычислить, какие выходные значения выдаст нейросеть на i -м примере, при помощи простой формулы. Мы хотим обучить нейрон и подбираем оптимальные веса, чтобы свести к минимуму ошибки при распознавании примеров. Можно сказать, мы хотим свести к минимуму квадратичную ошибку во всех примерах, которые встретим. Формально, если мы знаем, что t (i) — верный ответ на i -й пример, а y (i) — значение, вычисленное нейросетью, мы хотим свести к минимуму значение функции потерь E :

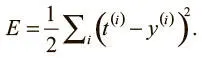
Квадратичная ошибка равна 0, когда модель дает корректные предсказания для каждого обучающего примера. Более того, чем ближе E к 0, тем лучше модель. Наша цель — выбрать такой вектор параметров θ (значения всех весов в этой модели), чтобы E было как можно ближе к 0.

Вы, возможно, недоумеваете: зачем утруждать себя функцией потерь, если проблему легко решить с помощью системы уравнений. В конце концов, у нас есть наборы неизвестных (весов) и уравнений (одно для каждого примера). Это автоматически даст нам ошибку, равную 0, если обучающие примеры подобраны удачно.

Хорошее замечание, но, к сожалению, актуальное не для всех случаев. Мы применяем здесь линейный нейрон, но на практике они используются редко, ведь их способности к обучению ограничены. А когда мы начинаем использовать нелинейные нейроны — сигмоиду, tanh или усеченный линейный, о которых мы говорили в конце предыдущей главы, — мы не можем задать систему уравнений! Так что для обучения явно нужна стратегия получше [9].

Визуализируем для упрощенного случая то, как свести к минимуму квадратичную ошибку по всем обучающим примерам. Допустим, у линейного нейрона есть только два входа (и соответственно только два веса — w 1и w 2). Мы можем представить себе трехмерное пространство, в котором горизонтальные измерения соответствуют w 1и w 2, а вертикальное — значению функции потерь E . В нем точки на горизонтальной поверхности сопоставлены разным значениям весов, а высота в них — допущенной ошибке. Если рассмотреть все ошибки для всех возможных весов, мы получим в этом трехмерном пространстве фигуру, напоминающую миску (рис. 2.2).

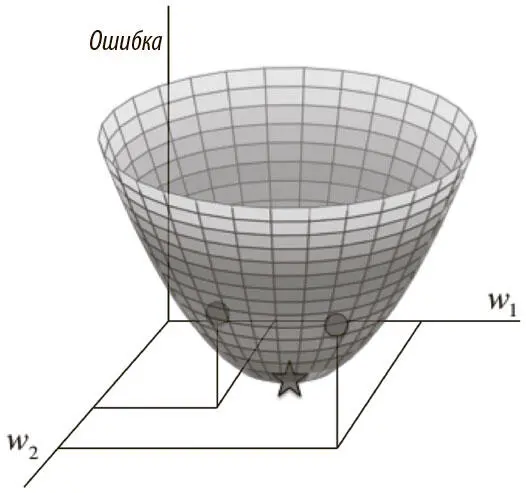
Рис. 2.2. Квадратичная поверхность ошибки для линейного нейрона

Эту поверхность удобно визуализировать как набор эллиптических контуров, где минимальная ошибка расположена в центре эллипсов. Тогда мы будем работать с двумерным пространством, где измерения соответствуют весам. Контуры сопоставлены значениям w 1и w 2, которые дают одно и то же E . Чем ближе они друг к другу, тем круче уклон. Направление самого крутого уклона всегда перпендикулярно контурам. Его можно выразить в виде вектора, называемого градиентом .

Пора разработать высокоуровневую стратегию нахождения значений весов, которые сведут к минимуму функцию потерь. Допустим, мы случайным образом инициализируем веса сети, оказавшись где-то на горизонтальной поверхности. Оценив градиент в текущей позиции, мы можем найти направление самого крутого спуска и сделать шаг в нем. Теперь мы на новой позиции, которая ближе к минимуму, чем предыдущая. Мы проводим переоценку направления самого крутого спуска, взяв градиент, и делаем шаг в новом направлении. Как показано на рис. 2.3, следование этой стратегии со временем приведет нас к точке минимальной ошибки. Этот алгоритм известен как градиентный спуск, и мы будем использовать его для решения проблемы обучения отдельных нейронов и целых сетей [10].