Мэри вышла в коридор. Она взялатам стакан с молоком. Затем она вернулась в офис, где увидела яблоко, и взяла его.
Сколько предметов в руках у Мэри?
Ответ тривиален: два! Но что в нашем мозге породило этот вариант? Если бы мы думали о том, как ответить на этот вопрос на понимание с помощью простой компьютерной программы, алгоритм, вероятно, выглядел бы так.
1. назначить ячейку памяти для подсчета .
2. инициализировать подсчет значением 0.
3. для каждого слова в тексте .
3.1. если слово — взяла.
3.1.1. увеличить число .
4. выдать значение.
Оказывается, мозг подходит к решению задачи почти так же, как и эта простая программа. Приступая к чтению, мы выделяем место в памяти (как и она) и помещаем туда полученные данные. Сначала мы фиксируем местоположение Мэри — судя по первому предложению, это коридор. Из второго получаем информацию о предметах, которые несет Мэри. Сейчас это стакан молока. Когда мы видим третье предложение, мозг модифицирует значение первой ячейки памяти: уже не коридор, а офис. К концу четвертого предложения вторая ячейка тоже модифицируется, вместив не только молоко, но и яблоко. Когда мы доходим до вопроса, мозг быстро обращается ко второй ячейке и получает оттуда информацию о том, что предметов два. В нейронауках и когнитивной психологии такая система кратковременного хранения информации и управления ею называется кратковременной памятью. Именно она лежит в основе исследований, которые мы будем рассматривать в этой главе.
В 2014 году Алекс Грейвз и коллеги из Google DeepMind впервые осветили этот вопрос в статье «Нейронные машины Тьюринга» [98], где ввели новую нейронную архитектуру под тем же названием — нейронная машина Тьюринга (Neural Turig Machine, NTM). Она состоит из контроллерной нейронной сети (обычно РНС) с внешним запоминающим устройством, созданным по принципу рабочей памяти мозга.
Рисунок 8.1 показывает, что то же сходство сохраняется и для архитектуры нейронной машины Тьюринга с внешней памятью вместо RAM, головками считывания/записи вместо шины считывания/записи и контроллера с сетью вместо CPU, за исключением того, что контроллер обучается программе, а в CPU она поступает в готовом виде.
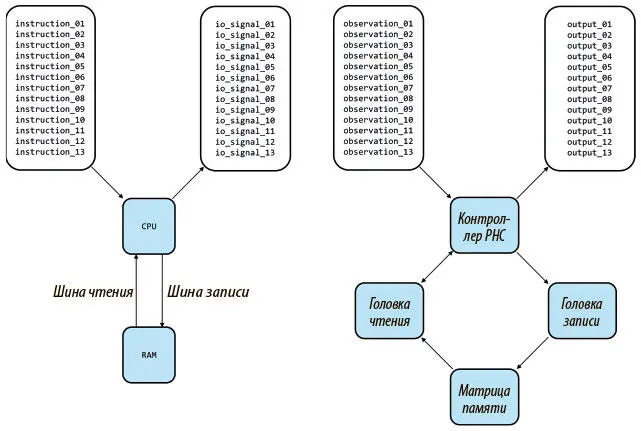
Рис. 8.1. Сравнение архитектуры современного компьютера, в который поступает готовая программа (слева), с нейронной машиной Тьюринга, которая обучается (справа). Здесь по одной головка чтения и записи, но в NTM их может быть и по нескольку
Если рассмотреть NTM в свете беседы о полноте РНС по Тьюрингу, окажется, что дополнение РНС внешней памятью для кратковременного хранения позволяет вырезать из поля поиска существенный сегмент. Ведь теперь не нужно работать с РНС, которые способны и манипулировать информацией, и хранить ее: достаточно найти те, которые могут обрабатывать информацию с внешнего носителя. Такое сужение поля поиска помогает нам частично раскрыть потенциал РНС, до которого ранее было тяжело добраться. Это очевидно по разнообразию задач, которым может научиться NTM: от копирования последовательностей входных данных до эмулирования н-граммных моделей и сортировки данных по приоритетам. К концу главы мы увидим, как расширенная NTM может научиться выполнять задачи на понимание прочитанного, вроде рассмотренной выше, методом градиентного поиска!
Доступ к памяти на основе внимания
Чтобы обучать NTM по методу градиентного поиска, нужно убедиться, что вся архитектура дифференцируема: можно вычислить градиент исходящих потерь по отношению к параметрам модели, обрабатывающим входные данные. Это свойство называется сквозной дифференцируемостью — от входа к выходу. Если мы попробуем получить доступ к памяти NTM так, как цифровые компьютеры обращаются к RAM, через дискретные значения адресов, мы получим разрывность в градиентах вывода и не сможем больше обучать модель градиентным методом. Нам нужен способ постоянного доступа к памяти и возможность «сосредоточиться» на конкретной ее ячейке. И такой постоянной концентрации можно достичь благодаря методам внимания!
Вместо дискретного адреса в памяти мы даем каждой головке возможность создать нормализованный функцией мягкого максимума вектор внимания того же размера, что и число ячеек памяти. Так мы получим доступ ко всем ячейкам памяти одновременно в размытом виде. Каждое значение вектора будет показывать, насколько мы собираемся концентрироваться на ячейке или насколько вероятно то, что нам понадобится доступ к ней. Например, чтобы прочесть вектор на временном шаге t из матрицы памяти N x W , обозначенной M t (где N — число ячеек, а W — размер ячейки), мы создаем вектор внимания, или вектор весов w t размера N , и вектор считывания можно будет вычислить через произведение 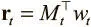 , где
, где 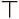 обозначает операцию транспонирования матрицы. Рисунок 8.2 показывает, как эти веса относятся к конкретной ячейке. Теперь мы можем извлечь вектор чтения, содержащий примерно ту же информацию, что и ячейка памяти.
обозначает операцию транспонирования матрицы. Рисунок 8.2 показывает, как эти веса относятся к конкретной ячейке. Теперь мы можем извлечь вектор чтения, содержащий примерно ту же информацию, что и ячейка памяти.
Читать дальше
Конец ознакомительного отрывка
Купить книгу


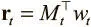 , где
, где 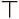 обозначает операцию транспонирования матрицы. Рисунок 8.2 показывает, как эти веса относятся к конкретной ячейке. Теперь мы можем извлечь вектор чтения, содержащий примерно ту же информацию, что и ячейка памяти.
обозначает операцию транспонирования матрицы. Рисунок 8.2 показывает, как эти веса относятся к конкретной ячейке. Теперь мы можем извлечь вектор чтения, содержащий примерно ту же информацию, что и ячейка памяти.










