Solución:En este circuito se observa que los resistores de 20 Ω están en paralelo con un cable (resistencia cercana a 0 Ω), por lo tanto, podemos ignorar esos resistores, ya que la resistencia equivalente 20||20||0 es 0 Ω. De igual manera, el resistor de 30 Ω, de la rama inferior, también está conectado en paralelo con un cable, por lo que se puede ignorar. El circuito resultante se muestra en la figura 2.10(a).
Ahora se puede hallar la resistencia equivalente entre los resistores de 20 Ω y 2 kΩ que se encuentran en paralelo, al lado derecho del circuito. El circuito resultante se muestra en la figura 2.10(b).
En el circuito resultante observamos que los resistores de 30 Ω, 3 Ω y 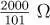 se encuentran en serie; su resistencia equivalente es . El circuito resultante se muestra en la figura 2.10(c).
se encuentran en serie; su resistencia equivalente es . El circuito resultante se muestra en la figura 2.10(c).
Ahora determinamos la resistencia equivalente entre el paralelo , tal como se muestra en la figura 2.10(d). En este circuito, las resistencias de están en serie y su resistencia equivalente es 57,25 Ω, tal como se observa en la figura 2.10(e).
Finalmente, la resistencia equivalente vista desde las terminales a y b corresponde al paralelo Rab = 57,25 Ω||57 Ω ⇒ Rab = 28,56 Ω.
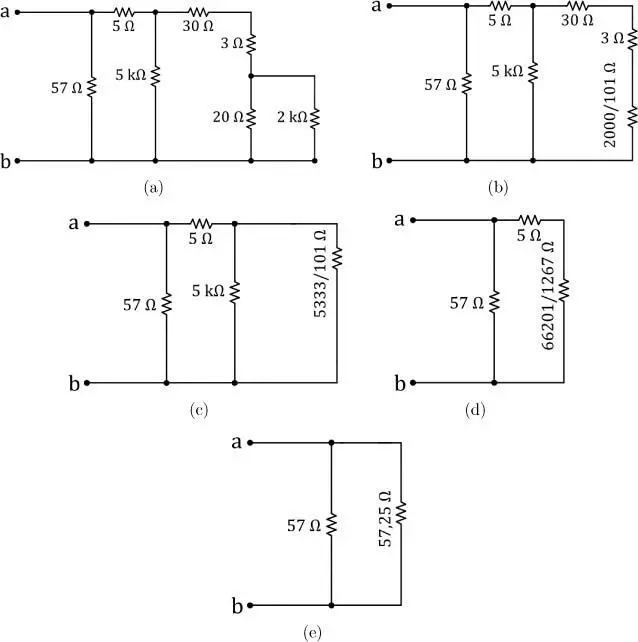
Figura 2.10: Solución del circuito eléctrico del ejemplo 2.1.2.
Las leyes de Kirchhoff junto con la ley de Ohm se utilizan para analizar eficazmente una gran variedad de circuitos eléctricos. Como se anotó, existen dos leyes de Kirchhoff: la ley de voltaje y la ley de corriente. Estas se expondrán en las siguientes secciones.
Esta ley establece que la suma algebraica de los voltajes de los elementos en un lazo debe ser igual a cero en todo instante de tiempo. Se usará LVK para referirnos a esta ley. En la figura 2.11se muestra un ejemplo de la aplicación de la LVK.
Ejemplo 2.2.1.Determine la corriente que circula por el circuito de la figura 2.11.
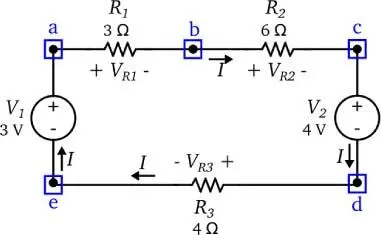
Figura 2.11: Aplicación de la LVK en un circuito eléctrico.
Solución:En este circuito, formado por un solo lazo, y con todos los elementos conectados en serie (circula la corriente I a través de todos los elementos), si se comienza el recorrido por el nodo e en sentido de las manecillas del reloj, la LVK nos arroja:
De acuerdo a la ley de Ohm, el voltaje en los resistores se puede expresar como V = RI , por lo tanto, la expresión anterior se puede expresar como:
Sustituyendo los valores de las variables conocidas obtenemos:
El signo negativo de la corriente indica que el sentido inicial de la corriente que se supuso al inicio no es el correcto, y por lo tanto, la corriente circula en sentido contrario.
De acuerdo a la LVK, las fuentes de voltaje conectadas en serie se pueden sumar algebraicamente y pueden ser reemplazadas por una única fuente de voltaje independiente, tal como se muestra en la figura 2.12. Las fuentes de voltaje independientes se pueden sumar entre sí, y las fuentes de voltaje dependientes se pueden sumar entre sí, pero no se pueden sumar fuentes dependientes con fuentes independientes.
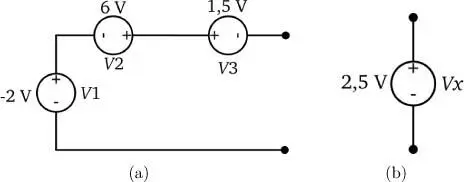
Figura 2.12: Las fuentes de voltaje independientes en serie (a) se pueden reemplazar en una única fuente de voltaje independiente (b) para simplificar el circuito y facilitar su análisis.
Esta ley establece que la suma algebraica de las corrientes que entran a un nodo debe ser igual a cero en todo instante de tiempo. Dicho en otros términos, la suma de las corrientes que entran a un nodo debe ser igual a la suma de las corrientes que salen del mismo nodo. Esta ley se puede abreviar como LCK. En la figura 2.13
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

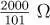 se encuentran en serie; su resistencia equivalente es . El circuito resultante se muestra en la figura 2.10(c).
se encuentran en serie; su resistencia equivalente es . El circuito resultante se muestra en la figura 2.10(c).













