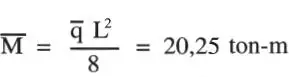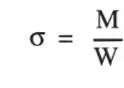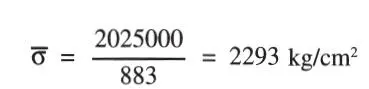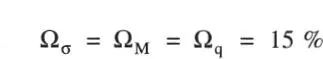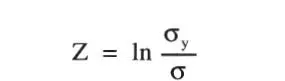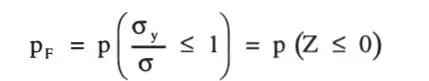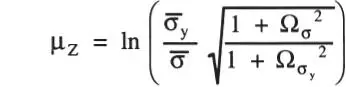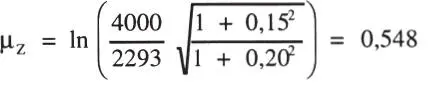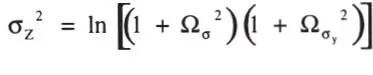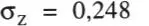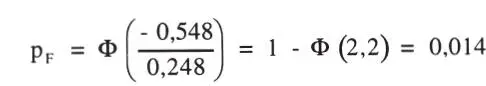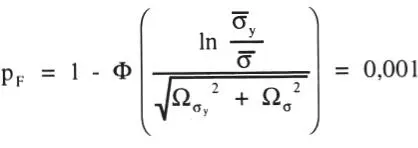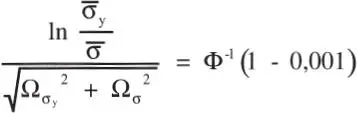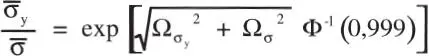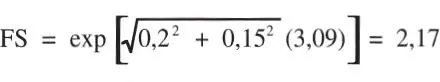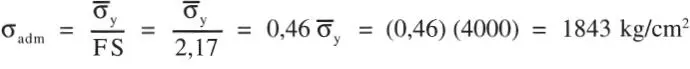Ejemplo 1.1
Sea una columna sometida a una carga axial de 40 toneladas correspondiente al peso propio de la estructura que soporta, con coeficiente de variación estimado en un 10 %, más una sobrecarga de 60 toneladas con coeficiente de variación estimado en un 25%. La columna se ha diseñado de manera que su resistencia última de compresión es el triple de la carga de servicio total. Asumiendo que el coeficiente de variación de la resistencia es de un 15 %, y que todas las variables son gaussianas y estadísticamente independientes, calcular la probabilidad de colapso de la columna utilizando la formulación conocida por margen de seguridad.
Solución:La carga total S = PP + SC es también gaussiana porque PP y SC lo son, por lo tanto:
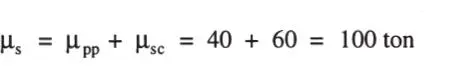
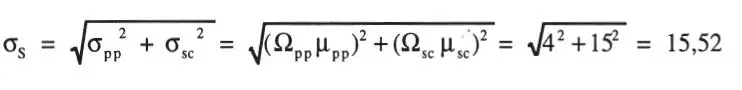
La resistencia última nominal es μ R= 300 toneladas con σ R= (0,15)(300) = 45 toneladas como desviación estándar. La probabilidad de falla según la Ec. 1-21 es:
Ejemplo 1.2
Una viga de acero simplemente apoyada de 9 metros de luz (perfil IN 35x53) soporta una carga uniformemente distribuida de intensidad media 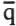 = 2 ton/m y coeficiente de variación Ω q= 15 %. El material de la viga tiene una tensión de fluencia media
= 2 ton/m y coeficiente de variación Ω q= 15 %. El material de la viga tiene una tensión de fluencia media  y= 4000 kg/cm 2y COV Ωσ y= 20 %. Suponiendo que q y σ ytienen distribución log-normal, determinar:
y= 4000 kg/cm 2y COV Ωσ y= 20 %. Suponiendo que q y σ ytienen distribución log-normal, determinar:
a) La probabilidad de falla, definida la falla como el evento de alcanzar o exceder la resistencia límite de fluencia.
b) La tensión admisible de flexión o el factor de seguridad central requerido para limitar a 1/1000 la probabilidad de falla.
Solución:a) El valor medio del momento flector máximo es:
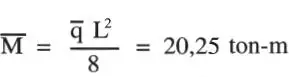
Como q es log-normal, M también lo es. La tensión máxima de flexión en una sección simétrica está dada por:
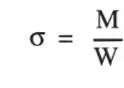
en que W es el módulo resistente de la sección, variable supuesta determinística. Por ser M log-normal, σ es log-normal. El perfil dado tiene W = 883 cm 3, luego:
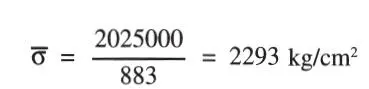
y:
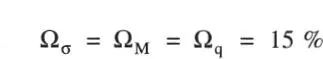
Definiendo la función rendimiento conforme a la formulación “factor de seguridad”:
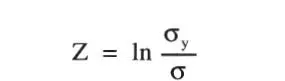
que tiene distribución normal (ver Ec. 1-25); la probabilidad buscada es:
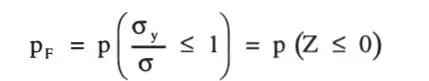
Utilizando las Ecs. 1-27 y 1-28 se obtienen la media μ zy la desviación standard σz:
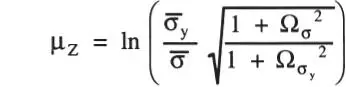
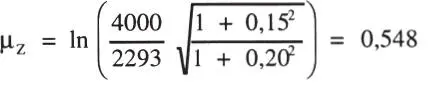
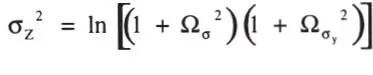
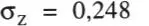
Entonces, según la Ec. 1-29, y de la Tabla P.1 se obtiene:
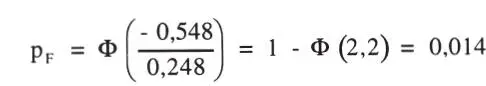
b) Se desea p F= 0,001, o sea, usando ahora la Ec. 1-30 se obtiene:
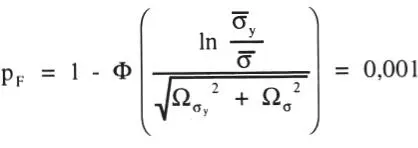
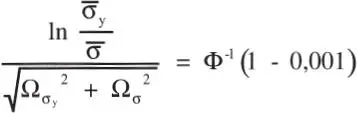
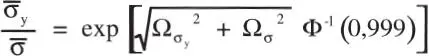
El cuociente del primer miembro de la ecuación anterior corresponde al factor de seguridad central, luego en este caso:
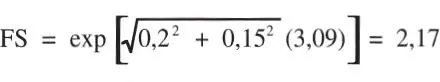
y la tensión admisible correspondiente a este factor de seguridad es:
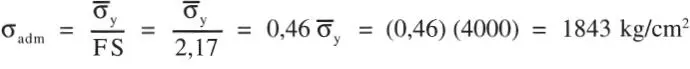
1.1.3 Criterios de Diseño para Seguridad
Dado el estado del arte actual, las normas de diseño están planteadas en términos determinísticos. Independientemente de que ciertos modelos probabilísticos han sido utilizados para definir la intensidad de las cargas, el enfoque es deterministico porque no se requiere hacer un análisis de confiabilidad estructural, es decir, evaluar la seguridad de un diseño (elemento o estructura completa) en términos de probabilidades. La situación actual resulta en diseños que no son consistentes con un nivel uniforme de seguridad, en el sentido que ciertos elementos pueden resultar diseñados en condiciones considerablemente más conservadoras, o inversamente más inseguras, que otros. Solamente un enfoque global probabilístico, tanto en los métodos de análisis con variables aleatorias, como en la consideración de las resistencias (incluyendo las incertidumbres implícitas en las propiedades de los materiales, diseño y construcción), puede conducir a un enfoque racional global. Este tipo de enfoque es por el momento parte del futuro.
En términos generales puede decirse que las normas enfocan el problema de seguridad según dos filosofías o criterios diferentes de diseño: el método de diseño elástico o de tensiones admisibles y el método de diseño a la rotura o de capacidad última.
a) Diseño Elástico o de Tensiones Admisibles
Este criterio establece que para las cargas de trabajo ningún punto de la estructura puede tener una tensión superior a un valor admisible” que garantice que la estructura se mantenga en el rango elástico.
Читать дальше


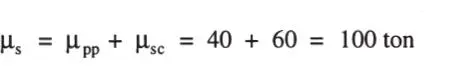
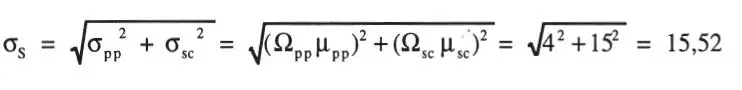
 = 2 ton/m y coeficiente de variación Ω q= 15 %. El material de la viga tiene una tensión de fluencia media
= 2 ton/m y coeficiente de variación Ω q= 15 %. El material de la viga tiene una tensión de fluencia media  y= 4000 kg/cm 2y COV Ωσ y= 20 %. Suponiendo que q y σ ytienen distribución log-normal, determinar:
y= 4000 kg/cm 2y COV Ωσ y= 20 %. Suponiendo que q y σ ytienen distribución log-normal, determinar: