Rafael Riddell C. - Diseño estructural

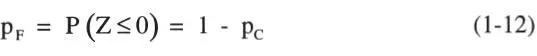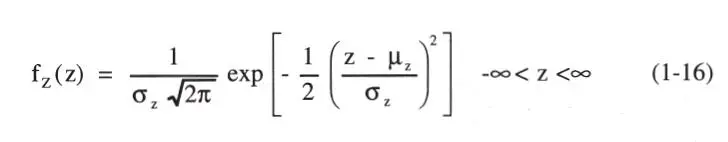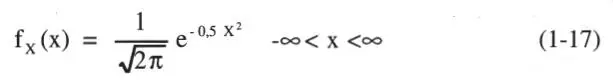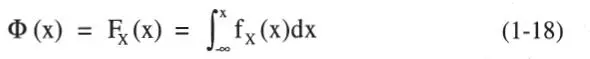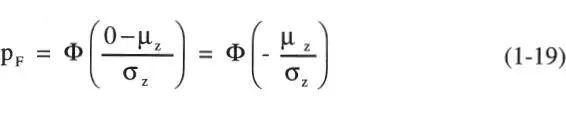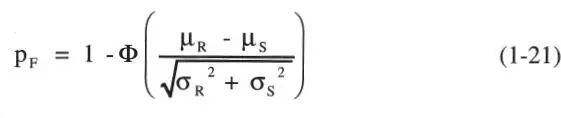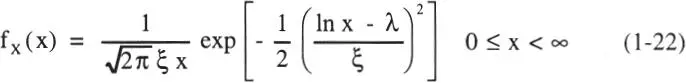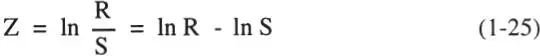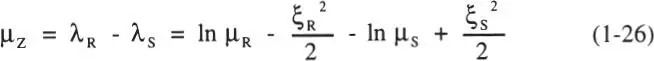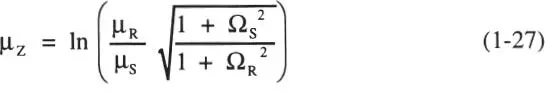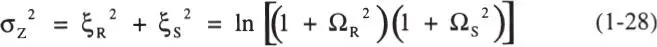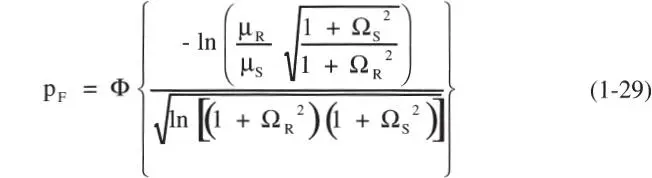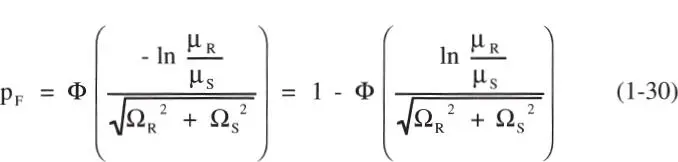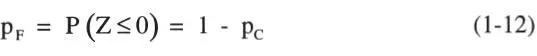
Si la FDP de Z es conocida, la probabilidad de falla según la Ec. 1-1 es simplemente:

Suponiendo que R y S son variables aleatorias estadísticamente independientes y normalmente distribuidas, con medias μ Ry μ Sy desviaciones estándar σ yσ Srespectivamente, es fácil demostrar que Z=R-S es también gaussiana con media:

y varianza:

Siendo Z normal, su FDP es:

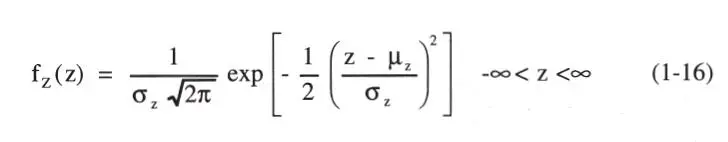
En notación abreviada se refiere a esta distribución como N(μ z,σ z). La integración definida por la Ec. 1-13 para el cálculo de la probabilidad de falla puede realizarse directamente; sin embargo, es usual realizar un cambio de variable para utilizar las tablas disponibles para la FDA Φ (x) de la distribución normal estandarizada a media nula y desviación estándar unitaria, es decir, la distribución N(0,1);

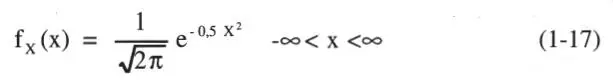
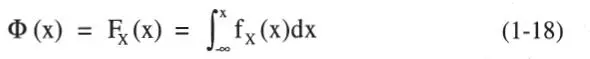
Entonces, haciendo x = (z-μ z,)/σ z, y dz = σ zdx la distribución de la Ec. 1-16 se estandariza a la N(0,1) dada por la Ec. 1-17. Por lo tanto, la integral de la Ec. 1-13 es:

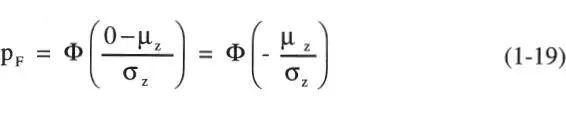
que por la simetría de la distribución N(0,1) puede escribirse como:

Finalmente, en virtud de las Ecs. 1-14 y 1-15:

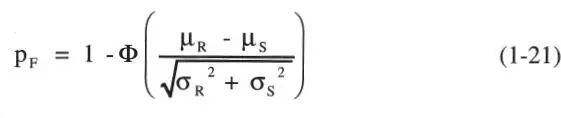
en que los valores de Φ se presentan en la Tabla P.1 del Anexo P. La Ec. 1-21 ilustra el importante hecho que la seguridad no sólo depende del margen entre Ry S, representado por sus valores medios, sino también de la dispersión o incertidumbre respecto del valor de tales variables. Este hecho se ilustra esquemáticamente en la Fig. 1.4, donde las líneas continuas representan funciones de distribución hipotéticas de R y S y las líneas de guiones distribuciones tales que los valores medios se han mantenido, pero las desviaciones estándar se han duplicado. El efecto es que ha aumentado el área traslapada entre ambas curvas, lo que refleja un aumento de la probabilidad de falla. Notar, sin embargo, que P Fno corresponde al área traslapada, pero si tal área crece, P Ftambién crece.

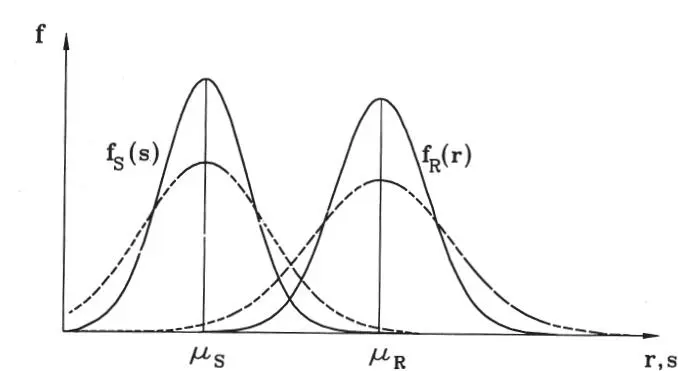
Figura 1.4Distribuciones esquemáticas de la resistencia Ry la solicitacións

Alternativamente la confiabilidad puede evaluarse mediante una formulación basada en el cuociente R/S, la que se asocia al concepto de factor de seguridad . En este caso es común asumir que Ry S son variables aleatorias independientes, con distribución log-normal. Cabe recordar que si una variable aleatoria X es lognormal, inX es normal, por tanto la FDP de X es:

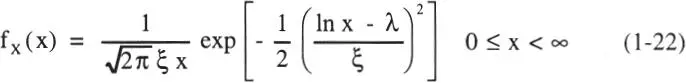
donde λ = E(InX) y ξ 2= Var(InX) son los parámetros de la distribución y corresponden respectivamente a la media y a la varianza de In X. Estos parámetros se relacionan con la media μ= E(X) y la varianza σ 2= Var(X) a través de las relaciones (Ang y Tang, 1975):

Si el coeficiente de variación Ω = σ /μ es pequeño, ξ ≈ Ω

Refiriendo la seguridad en términos de la variable aleatoria Z tal que:

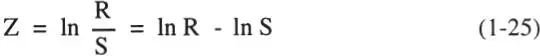
variable que tiene distribución normal pues Ry S se asumieron log-normales, el estado de falla se asocia a la condición (R-S) ≤ 0, es decir Z ≤ 0, y la probabilidad de falla queda igualmente expresada por las Ecs. 1-12 y 1-19.

De las Ecs. 1-25 y 1-23 se tiene que la media de Z es:

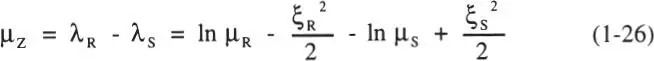
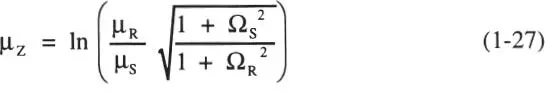
y su varianza:

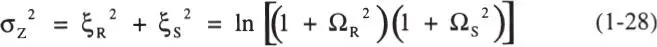
Luego, la probabilidad de falla según la Ec. 1-19 es:

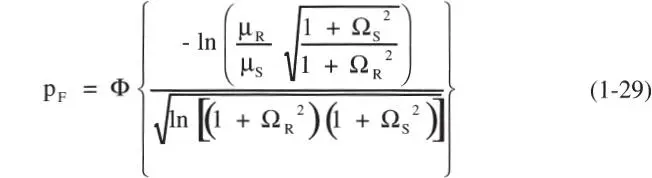
Si Ω Ry Ω sson pequeños (≤ 0,3), la raíz del numerador en la ecuación anterior puede aproximarse a 1, y el denominador a (Ω R 2+ Ω S 2) 1/2, de modo que:

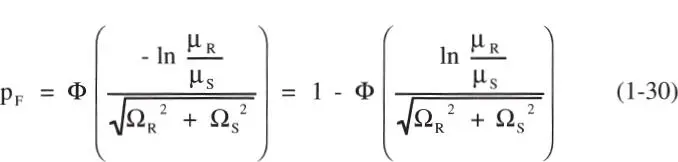
Al cuociente μ R/ μ Sse le denomina usualmente factor de seguridad central , mientras que Ω = (Ω R 2+ Ω S 2) 1/2corresponde a la incertidumbre total subyacente al diseño.

Para tener una idea del significado de los valores de las probabilidades de falla, puede considerarse que p F> 10 -3revela una situación de alto riesgo, posiblemente inaceptable, mientras que p F< 10 -5refleja una condición de bajo riesgo. Cabe notar también que para valores pequeños de la probabilidad de falla, ésta es muy sensible a la distribución considerada para la variable Z, lo que puede exigir utilizar la correcta FDP de Z para una determinación realista del riesgo. Sin embargo, aun cuando se use una distribución aproximada, las probabilidades de falla calculadas son aún útiles como medidas relativas de la seguridad. Valores grandes de PF, en cambio, no varían sustancialmente al cambiar la FDP de Z; sin embargo, en este caso se requiere una acción inmediata para reducir el riesgo. Para poner los valores de las probabilidades de falla en la perspectiva de otras situaciones de riesgo, la Tabla 1.2 muestra las tasas anuales de muerte en varias actividades.