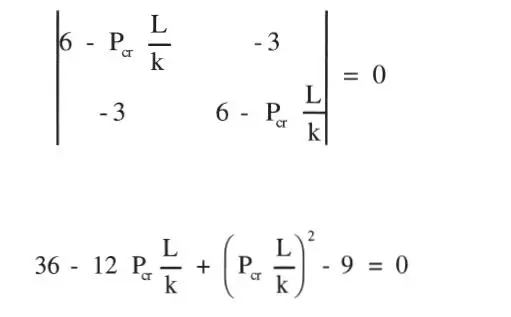
ecuación característica cuyas soluciones son:
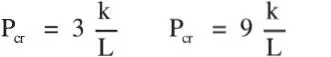
de estas soluciones, la menor es la relevante para efectos de diseño.
1.3 EJERCICIOS PROPUESTOS
1.01Para analizar la seguridad de un talud de tierra se supone el arco circular con centro en O como superficie de falla potencial. Las resistencias totales al deslizamiento que proveen los suelos 1 y 2 son R 1y R 2respectivamente de modo que el momento resistente es MR = r(R 1+ R 2). El momento solicitante es M s= aW, en que W es el peso de la cuña de suelo limitada por la superficie de falla. Se da la siguiente información: 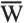 = 200 ton,
= 200 ton, 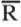 1= 50 ton,
1= 50 ton, 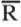 2= 200 ton, σ w= 20 ton, σ R1= 20 ton y σ R2= 50 ton. Suponiendo que las variables indicadas son estadísticamente independientes, se pide: a) Evaluar la probabilidad de deslizamiento, utilizando la formulación de margen de seguridad, y b) Determinar el peso máximo de una estructura que se desea construir sobre el terraplén sin que se exceda una probabilidad de falla de 0,003.
2= 200 ton, σ w= 20 ton, σ R1= 20 ton y σ R2= 50 ton. Suponiendo que las variables indicadas son estadísticamente independientes, se pide: a) Evaluar la probabilidad de deslizamiento, utilizando la formulación de margen de seguridad, y b) Determinar el peso máximo de una estructura que se desea construir sobre el terraplén sin que se exceda una probabilidad de falla de 0,003.
1.02¿Qué se entiende por resistencia característica de un material? Dé ejemplos.
1.03¿Qué se entiende por capacidad o resistencia última nominal? ¿Cómo se relaciona con la resistencia última de un elemento real?
1.04Explique dos diferencias fundamentales entre los métodos de diseño “por tensiones admisibles” y por "capacidad última" en relación con la forma de aplicar el factor de seguridad.
1.05En diseño último, según el código ACI, para la combinación de cargas permanentes con sobrecargas se utilizan los factores de mayoración de 1,4 y 1,7 respectivamente. ¿Por qué estos factores son distintos?
1.06Defina área tributaria y explique por qué la carga sobre un elemento puede reducirse en la medida en que aumente el área tributaria.
1.07Rehacer el Ejemplo 1.4, considerando que la viga no es rígida. Usar los datos siguientes: a = 80 cm, viga de sección rectangular de 1 cm de ancho y 3 cm de alto, alambres de 0,031 cm 2de sección, módulo de elasticidad de todos los elementos E=2,1x10 6kg/cm(Respuesta: T 1=0,952 P; T 2=0,032 P; R = 0,016 P).
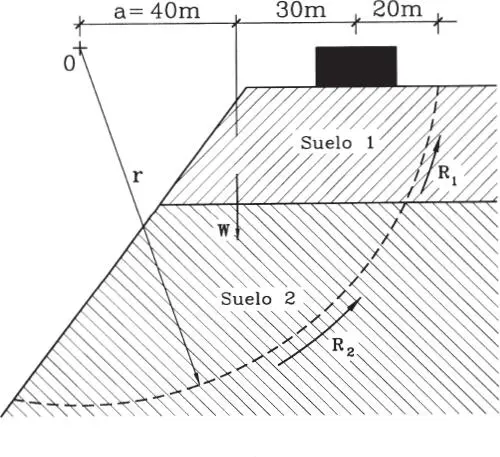
1.08En el sistema de la figura todos los elementos tienen módulo de elasticidad E, y las barras BC y DE son infinitamente rígidas a la flexión. Se pide: a) Determinar xey para que las barras BCy DE sólo se desplacen verticalmente sin girar, y b) Idem al caso anterior, pero cuando BC no es infinitamente rígida, sino que tiene momento de inercia dado I. Nota: En una viga simplemente apoyada de luz “L” la deflexión bajo una carga puntual P es δ = Pa 2(L-a) 2/3EIL, en que “a” es la distancia de la carga al extremo de la viga.
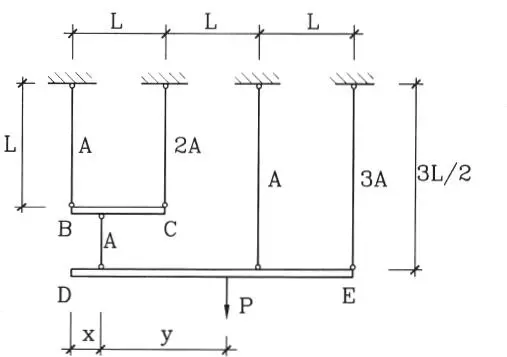
1.09La viga sin peso de la figura tiene un módulo de elasticidad E, momento de inercia I, y posición horizontal cuando está descargada, el resorte en B tiene constante ky no ejerce fuerza alguna cuando la viga está horizontal. Calcular el momento flector en A cuando se aplica una carga uniformemente distribuida de intensidad q por unidad de longitud.
(Respuesta: M = 3kqL 5/ (24EI + 8kL 3) - qL 2/2)
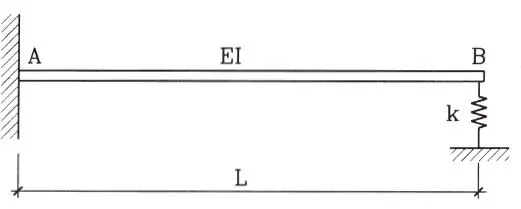
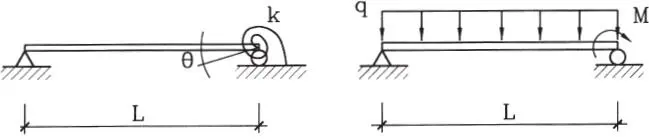
1.10La viga de la figura tiene apoyos simples y un resorte lineal elástico de constante k, que restringe el giro 0 del extremo B imponiendo un momento M=kθ. Utilizando la ecuación diferencial de la viga M(x)=Ely”, determine el momento que ejercerá el resorte cuando sobre la viga actúa una carga q uniformemente distribuida. Discutir los casos límites k = 0 y k =∞. (Respuesta: M = qkL 3/ 8(3EI + KL))
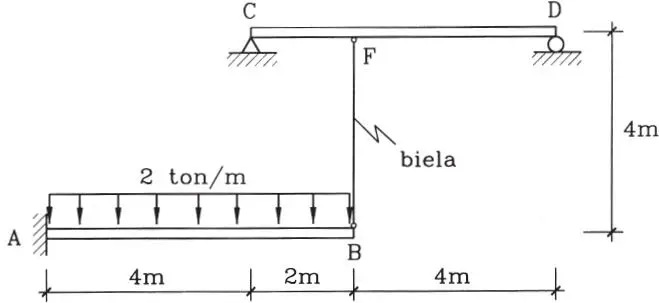
1.11Las vigas AB y CD de la figura son de acero (E = 2,1x10 6kg/cm 2) y están unidas por la biela BF del mismo material, en la forma indicada. El momento de inercia de la sección de las vigas es I = 18000 cm 4y el área de la sección de la biela es A = 0,785 cm 2(d = 10 mm). Sobre la viga AB se aplica una carga de 2 ton/m. Se pide: a) El diagrama de momentos de la viga CD, y b) Dibujar la deformada de la viga AB (considerando la deflexión vertical de los puntos A y B y por lo menos unos 4 puntos intermedios). (Respuesta: M max= 5,1 ton-m; δ B= 1,29 cm)
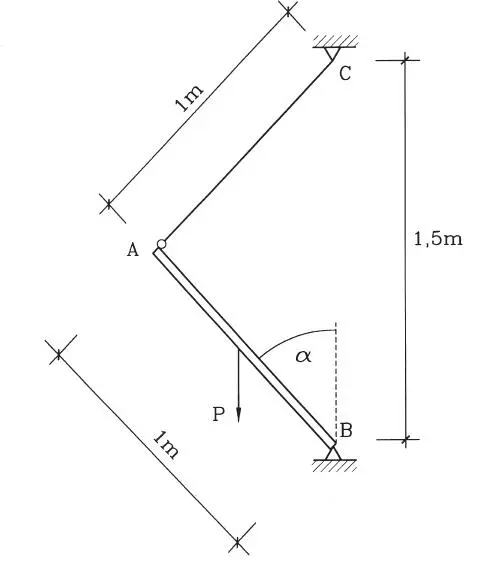
1.12La barra uniforme rígida AB, de peso P = 30 kg, está articulada en By sostenida por el elástico AC. La longitud de la barra y del elástico es de 1 m, de modo que la posición de equilibrio mostrada en la figura corresponde al caso en que el elástico es infinitamente rígido. Se pide determinar el ángulo de de equilibrio, y la fuerza axial que ejerce el elástico cuando éste es deformable y tiene rigidez k = 0,5 kg/cm. (Respuesta: 55,77° y 12,5 kg)
1.13Tres alambres unidos a una barra rígida sostienen una carga de 150 kg. ¿Qué carga soportará cada alambre si el de la derecha aumenta su temperatura en 45 °C? Las propiedades de los alambres son: A = 0,07 cm 2; E = 2,0×10 6kg/cm 2; α = coeficiente de dilatación = 12x10 -61/°C, L y a cualquiera (Respuesta: T 1= T 3= 37,4 kg; T 2= 75,2 kg).
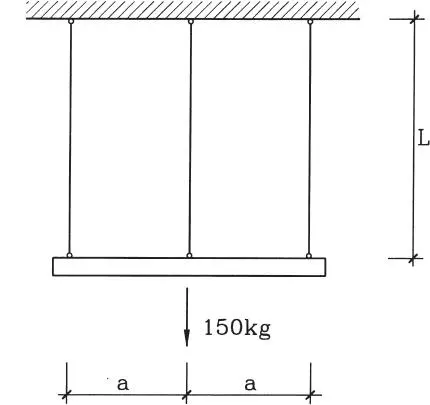
1.14Para la misma estructura y propiedades del ejercicio anterior, sometida a temperatura uniforme, ¿qué carga soporta cada alambre si el de la izquierda fue fabricado 0,0004 L más largo que los otros? (Respuesta: T 1= T 3= 40,66 kg; T 2= 68,67 kg).
1.15El acero utilizado para el hormigón armado y en estructuras metálicas es en general un material dúctil. a) ¿A qué se refiere la propiedad de ductilidad?, b) i puede este mismo acero comportarse en forma frágil en ciertas circunstancias, y c) ;existen aceros frágiles para uso estructural y no estructural?
Читать дальше

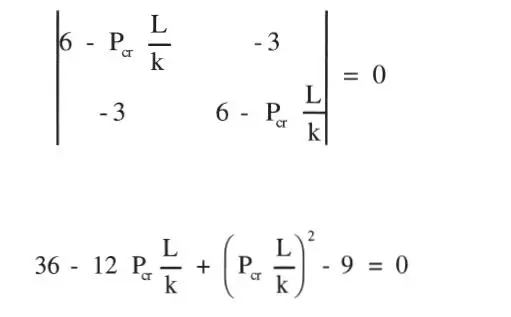
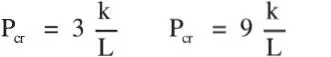
 = 200 ton,
= 200 ton,  1= 50 ton,
1= 50 ton, 

















