Rafael Riddell C. - Diseño estructural

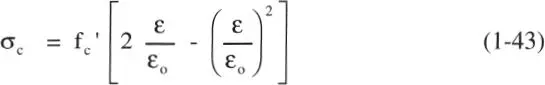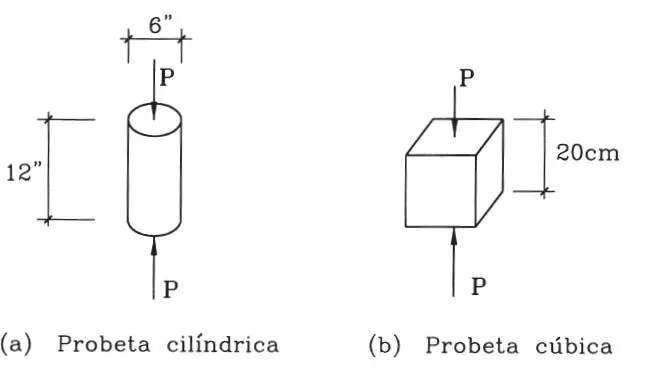
Figura 1.15Probetas estándar para el ensayo de compresión en hormigón

Como la resistencia del hormigón aumenta con el tiempo, tanto f ccomo f c’ se refieren convencionalmente a la edad de 28 días. Los ensayos se realizan a una velocidad de deformación unitaria relativamente lenta, del orden de 0,001/min, de modo que la resistencia máxima se alcanza en 2 ó 3 minutos. En ensayos muy rápidos, en que la carga máxima se alcanza en fracciones de segundo, se observan incrementos en la resistencia y en el módulo de elasticidad del orden de un 15 %.

La Fig. 1.16 muestra curvas σ-ε típicas para hormigones en ensayos lentos con control de deformación, lo que permite obtener la curva completa después de alcanzada la resistencia máxima. Varias observaciones de interés se pueden hacer en relación con esta figura: (a) el hormigón es un material frágil de muy baja capacidad de deformación que no tiene punto de fluencia ni rango de deformación plástica, (b) a mayor resistencia tiene menor capacidad de deformación, (c) la resistencia máxima se produce para ε ≤ 0,002, (d) después de alcanzada la resistencia máxima la capacidad del hormigón decae debido a su deterioro, que se manifiesta en grietas visibles paralelas a la dirección de la carga, las que se traducirían en una falla explosiva al alcanzar fc’ si el aparato de ensayo no redujera de inmediato la carga aplicada, (e) el colapso global de la probeta ocurre finalmente para ε ≥ 0,003, (f) la parte inicial de la curva σ-ε es aproximadamente lineal hasta σ ≈ 0,5 f c’, y (g) la curva σ-ε tiene en general forma parabólica.

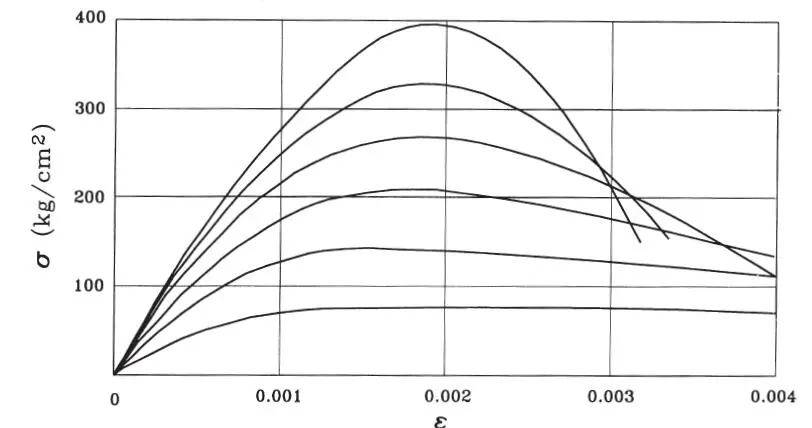
Figura 1.16Curvas de ensayos de compresión uniaxial en probetas cilíndricas (adaptada de Park y Paulay, 1975)

Para efectos de análisis se han propuesto varias idealizaciones de la relación tensión deformación del hormigón. La más popular es la de Hognestad, 1951 (Fig. 1.17), que utiliza entre ε = 0 y ε 0una forma parabólica dada por:

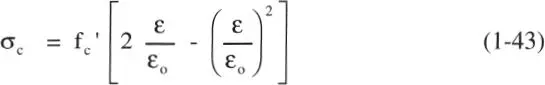
y una rama lineal entre ε o. y ε ucon tensión de fractura del hormigón σ u= 0,85 f c’ para ε = ε u. Hognestad propuso ε o= 2f c’/E cy ε u= 0,0038, sin embargo, es usual utilizar ε s≈ 0,002 y ε u≈ 0,003, sin perjuicio de cambiarlos en análisis específicos que lo requieran. También se usa frecuentemente, especialmente en Europa, la llamada “parábola-rectángulo”, cuya diferencia con la Fig. 1.17 es que mantiene σ c= f c’ para ε > ε o. El módulo de elasticidad, válido sólo en el rango lineal inicial de la curva σ-ε, queda dado por la Ec. 1-38, con una dispersión de ± 20 %; valores de E cdel orden de 220.000 a 280.000 kg/cm 2son típicos para el rango usual de resistencias, es decir, aproximadamente 1/10 a 1/8 del módulo de elasticidad del acero.

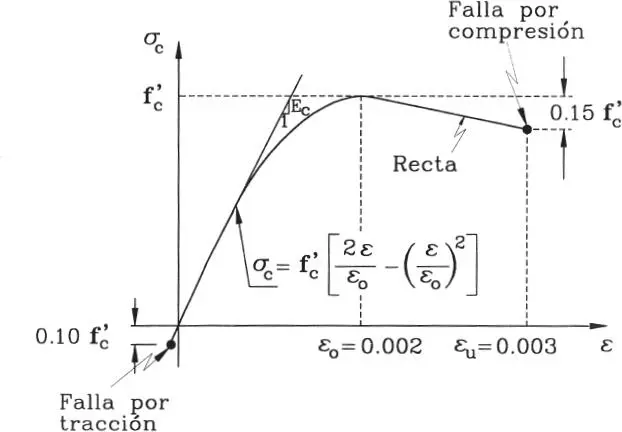
Figura 1.17Relación tensión-deformación idealizada del hormigón

La resistencia del hormigón a la tracción es muy baja, del orden de 10 a 15 % de f c’, y es muy dependiente del tipo de ensayo utilizado para medirla. El ensayo de tracción directa es complejo de realizar, por ello es más común el de flexotracción, que proporciona la resistencia de tracción en flexión o módulo de ruptura f r. Es generalmente aceptada la relación:

en que f ry f c’ deben expresarse en kg/cm 2.

Debido a la baja resistencia a la tracción del hormigón es usual ignorarla en los cálculos de resistencia del hormigón armado. Esto no significa que sea una propiedad poco importante del hormigón; de hecho no sólo hay casos especiales en que el hormigón se diseña en estado elástico controlado por su resistencia a la tracción, por ejemplo, en fundaciones sin armar o en estanques expuestos a fluidos altamente corrosivos o en pavimentos, sino también la resistencia a la tracción es una propiedad fundamental en relación con la resistencia al esfuerzo de corte del hormigón y en fenómenos de fisuración por retracción y temperatura.

1.2.2.3 Madera Aserrada

Las propiedades mecánicas de la madera presentan gran variación, dependiendo de la especie, la zona donde se desarrolla el árbol, el contenido de humedad de la madera y el tipo de solicitación.

Es de conocimiento común que ciertas especies como el roble y el eucaliptus son particularmente densas y resistentes, mientras lo contrario ocurre con el pino y el álamo. Sin embargo, el crecimiento del árbol es muy dependiente de las condiciones ambientales (temperatura, precipitación, calidad del suelo, manejo forestal, asoleamiento) de manera que no sólo las propiedades de una especie pueden variar considerablemente dependiendo de la localidad en que se ha desarrollado el árbol, sino que aún, en una misma localidad, son de hecho muy heterogéneas.

La Tabla M. 1 presenta algunos datos a modo de ejemplo (más información puede encontrarse en la referencia original, Instituto Forestal, 1967). Las propiedades mecánicas de la madera se presentan en términos de Op, la tensión en el límite de comportamiento lineal o límite de proporcionalidad, la tensión o, de ruptura (Fig. 1.19), el módulo de elasticidad E, y las tensiones de rotura a cizalle radial y tangencial (ambos paralelos a las fibras longitudinales de la madera, pero con plano de cizalle radial, perpendicular a los anillos de crecimiento, o tangencial, tangente a los anillos de crecimiento). Se puede observar en la Tabla M.1 que para una misma muestra de madera las propiedades en flexión, compresión y tracción son muy disímiles; básicamente, ésta es la característica de los materiales llamados anisotropos, cuyas propiedades físicas y mecánicas varían según la dirección considerada.

La presencia de agua en la madera tiene varias implicancias de interés. Como todo tejido vivo, la madera contiene una fuerte proporción de agua. Parte de esta agua está en combinación en las sustancias constituyentes de la madera y permanece constante en cantidad. Existe además una cantidad de agua que no forma parte integrante de la madera, que puede eliminarse por secamiento y que constituye la humedad de la madera . Esta humedad se presenta en dos formas: como humedad de saturación de las fibras, retenida por las membranas celulósicas, y como agua libre, contenida en los espacios intercelulares. La madera del árbol recién cortado tiene un alto contenido de humedad, entre 40 y 250 %, medida en relación con el peso seco de la madera como se indica más adelante. Cuando se elimina toda el agua libre, la humedad llega al punto de saturación de las fibras, que en todas las especies es de aproximadamente 30 %. El agua libre no tiene influencia sobre el volumen de la madera; por el contrario el agua de saturación es de la mayor importancia al considerar las contracciones de la madera. En efecto, cuando la humedad baja del 30 %, la madera empieza a contraerse y estas contracciones son proporcionales a la humedad perdida bajo el 30 %. La madera se contrae más tangencialmente (ε θ= reducción del perímetro de los anillos de crecimiento) que radialmente (ε r=reducción del tronco en dirección radial), mientras la contracción longitudinal (ε l = paralelo a las fibras) es insignificante (Fig. 1.18). Estas deformaciones varían considerablemente con la especie, valores típicos para 0 % de humedad son ε θ=0,08; ε r= 0,04 y ε l = 0,002, y para 15 % de humedad ε θ= 0,04; ε r=0,015; ε l = 0,001. Inversamente, la madera se hincha al aumentar su contenido de humedad, comportamiento que queda gobernado por las mismas relaciones que rigen la contracción.