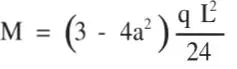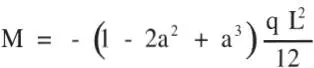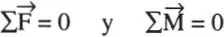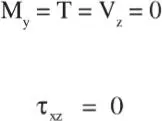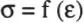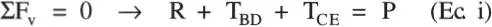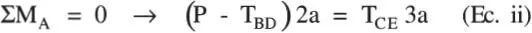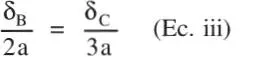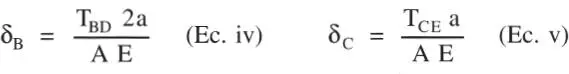Rafael Riddell C. - Diseño estructural

Solución:a) Para la viga simplemente apoyada el momento máximo al centro de la viga es:

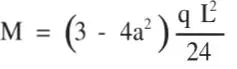
Para a= 1/4 se obtiene M=0,1146qL 2 y Q=3qL/4. Para esta última carga aplicada en forma uniforme (q’=Q/L = 3q/4) el momento flector máximo es M’ = q’L 2/8 = 0,0938qL 2, es decir, si en vez del caso real se supone que la carga es uniforme, el momento máximo se subestima en un 18 %. Si la carga es triangular M=qL 2/12 y Q=qL/2. Si esta carga se distribuye uniformemente (q' = 0,59), el momento flector máximo es M' =qL 2/16; en este caso suponer la carga uniforme en vez de triangular subestimaría el momento máximo en un 25 %.

b) Para la viga doblemente empotrada el momento en el empotramiento es:

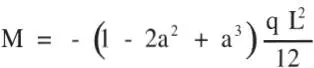
Para a = 1/4 se obtiene M=-0,0742qL 2. Si la carga se distribuye en forma uniforme M = -0,0625qL 2. La diferencia en este caso es del 16 %. Para la carga triangular M = -0,052. Si la carga se reparte uniformemente M = -0,042, subestimándose el momento en un 19 %.

1.2 PRINCIPIOS DE MECANICA ESTRUCTURAL

1.2.1 El Método de la Resistencia de Materiales

Una parte fundamental del diseño es el “análisis de tensiones” que comprende la determinación de las tensiones en la sección de elementos sometidos a distintos tipos de solicitación. Este tipo de análisis, que se realizará con mucha frecuencia a lo largo del curso es típicamente uno de naturaleza estáticamente indeterminada, es decir, las ecuaciones de equilibrio son insuficientes para resolverlo y es necesario recurrir a herramientas adicionales. El método de la Resistencia de Materiales usa tres herramientas básicas para resolver cualquier problema de mecánica estructural: equilibrio, geometría, y relaciones tensión-deformación. Estas herramientas, analizadas en detalle en el curso de Mecánica de Sólidos, se resumen a continuación:

• Condiciones de equilibrio: para cualquier cuerpo en equilibrio y para cualquier parte de este cuerpo debe cumplirse:

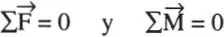
Por ejemplo, si se aplica este principio al equilibrio que debe existir entre los esfuerzos internos y las tensiones resultantes en una sección de un elemento, se puede escribir en componentes (Fig. 1.10):

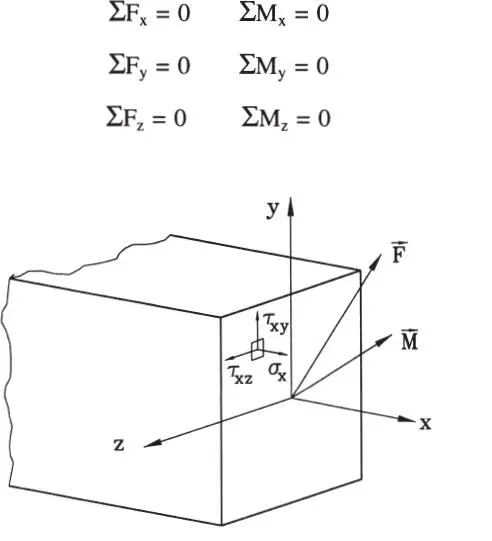
Figura 1.10Sección de un elemento estructural

En estas fuerzas y momentos intervienen la resultante de las acciones en la sección (esfuerzos internos M yy M zde flexión, M x= T de torsión, V yy V zde corte, y F x= P esfuerzo normal o axial) y las tensiones en la sección. Simplifiquemos el problema y supongamos que las cargas actúan simétricamente con respecto al plano XY. Si además se considera una sección simétrica se tiene:

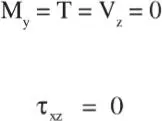
luego:

Si se grafican las intensidades σ xy τ xyperpendicularmente al plano de la sección, tanto P como V yson equivalentes al volumen encerrado por la superficie de tensiones y la cara de la sección.

• Compatibilidad geométrica: ésta indica que el conjunto de desplazamientos debe satisfacer la compatibilidad en los vínculos externos y la continuidad interna de la estructura en estudio.

• Relaciones tensión-deformación: aquí es donde se manifiesta el material de que está hecha la estructura. En el método de la resistencia de materiales estas relaciones se expresan a través de la curva tensión-deformación, la cual se obtiene usualmente para solicitación de tracción o compresión puras. En general se expresa como:

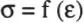
Los materiales estructurales tienen un rango en que la tensión σ es proporcional a la deformación unitaria ε para valores moderados de la tensión. Dentro de este rango se puede escribir σ = Eε, llamada usualmente Ley de Hooke, en que E es una propiedad del material denominada módulo de elasticidad. Esta relación es la base de cualquier teoría elástica. Si se desea incluir el comportamiento inelástico, es necesario considerar toda la curva, más allá de su límite elástico, como se verá más adelante.

A continuación se resolverán dos ejemplos sencillos para hacer hincapié en la metodología de solución, destacando que problemas de aparente naturaleza muy distinta, se resuelven utilizando apropiadamente las mismas herramientas básicas antes descritas.

Ejemplo 1.4

Determinar los esfuerzos en los alambres BD y CE de la estructura estáticamente indeterminada de la figura. Desarrollar una solución aproximada suponiendo que la viga AC es infinitamente rígida. Los alambres BD y CE tienen sección de área A y módulo de elasticidad E.

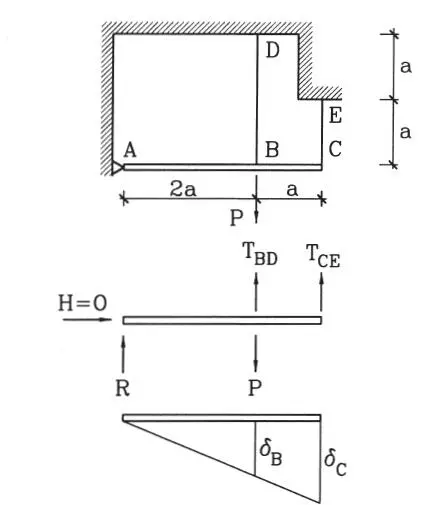
Figura E1.4

Solución:Equilibrio. Considérese el diagrama de cuerpo libre de la barra AC. Sean T BDy T CElas fuerzas en los alambres, que se supone están traccionados:

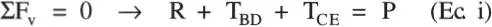
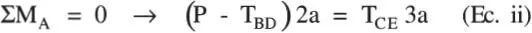
Es claro que las ecuaciones de equilibrio son insuficientes para resolver el problema pues hay 3 incógnitas y 2 ecuaciones.

Compatibilidad geométrica. Debido a que la barra AC es rígida:

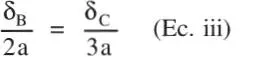
lo anterior implica dos nuevas incógnitas y una sola ecuación adicional.

Relaciones tensión-deformación. Aplicando la ley de Hooke a ambos alambres:

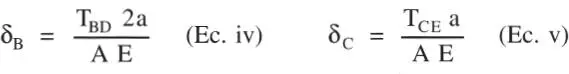
Después de esta etapa se completa el número de ecuaciones necesarias (5) para igual número de incógnitas. Luego, resolviendo el sistema de ecuaciones se obtienen: