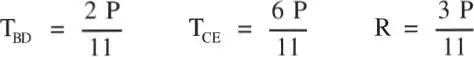
Ejemplo 1.5
Determinar las tensiones debidas a flexión en una sección con un plano de simetría, cargada en dicho plano.
Solución: Considérese una viga cargada en la forma indicada en la Fig. E1.5.a y una sección en el tramo central que está sometida a un momento flector constante (Fig. E1.5.b). Las seis ecuaciones de equilibrio son:

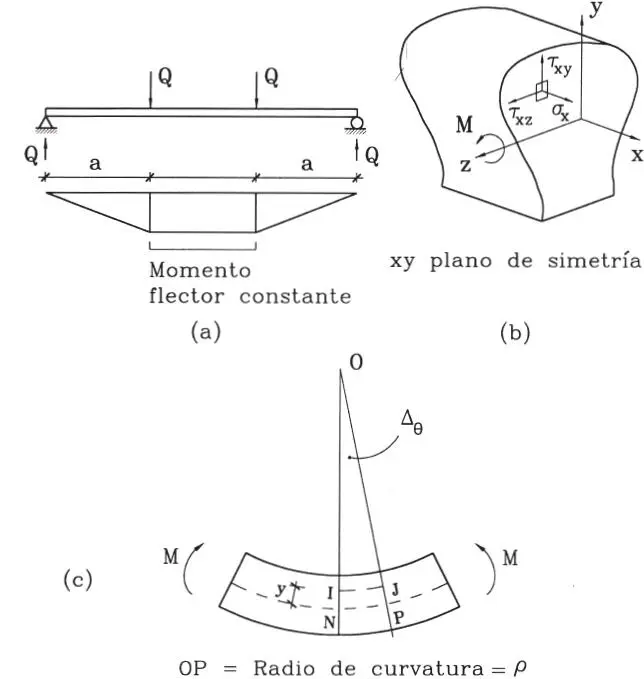
Figura E1.5
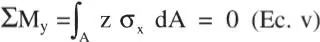
que se satisface automáticamente por la simetría respecto al plano XY, ya que el momento de σ xdA en z+, es igual al momento de σ xdA en z-.
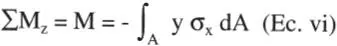
Las ecuaciones relevantes son la i y la vi que corresponden a las condiciones que debe satisfacer la distribución de tensiones σ x, buscada. Notar que este problema es esencialmente hiperestático, ya que se podría pensar que tiene infinitas incógnitas: el valor de σ xen los infinitos puntos de la sección.
Geometría. La condición de que las secciones planas permanecen planas en la flexión permite reducir la hiperestaticidad del problema a un grado. En efecto, considerando que dos secciones vecinas sólo giran relativamente en Δ θ(Fig. E1.5.c), se puede determinar la deformación unitaria de una fibra cualquiera de la sección (IJ) a distancia “y” del eje neutro:
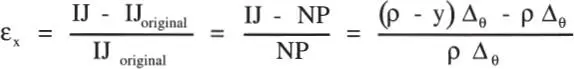
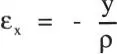
es decir, la única incógnita del problema es la deformación representada por ρ.
Relaciones tensión - deformación. En el rango de comportamiento elástico del material se cumple:
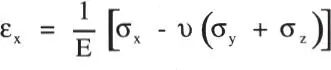
que bajo el supuesto σ y=σ z= 0 implica:
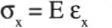
luego:
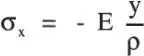
que reemplazado en la Ec.i da:
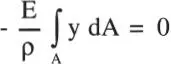
de donde se concluye que la superficie neutra pasa por el centro de gravedad de la sección. A su vez, reemplazando σ xen la Ec. vi se tiene:
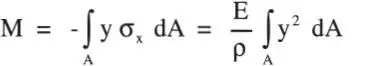
Definiendo:
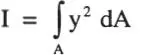
propiedad de la sección llamada momento de inercia , y sustituyendo en la expresión anterior para M, se obtiene:
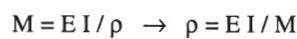
y finalmente:
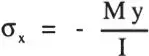
Similarmente al Ejemplo 1.5 se puede derivar la distribución de tensiones para el caso de flexión en vigas asimétricas sometidas a un momento en el plano YZ 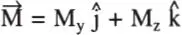 (Fig. 1.11). Se obtiene (Crandall y Dahl, 1972):
(Fig. 1.11). Se obtiene (Crandall y Dahl, 1972):
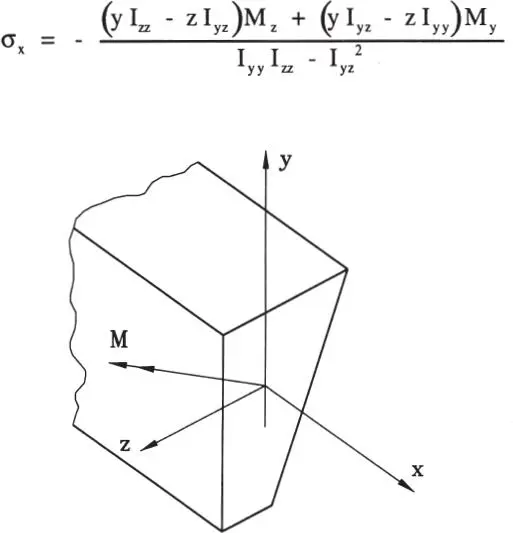
Figura 1.11Flexión en vigas con sección asimétrica
En los dos ejemplos anteriores se utilizaron las tres herramientas básicas de la mecánica estructural, que sirven para resolver cualquier problema:
• Equilibrio.
• Compatibilidad geométrica.
• Relaciones tensión - deformación.
La finalidad de los problemas era distinta. En el Ejemplo 1.4 se necesitaba calcular esfuerzos redundantes, y en el Ejemplo 1.5 se hizo un análisis de tensiones. En ambos casos se utilizó la misma metodología.
1.2.2 Relaciones Tensión-Deformación de los Materiales Estructurales
1.2.2.1 Acero Estructural
El ensayo de tracción uniaxial se realiza sobre una muestra de acero o probeta que se prepara dejando una zona central de sección A perfectamente constante mientras los extremos se ensanchan para permitir tomarla con las mordazas de la máquina que ejercerá la fuerza de tracción. La sección varía gradualmente con el propósito que así también lo hagan las tensiones de tracción, de modo que en la zona central éstas sean uniformes. A su vez, en la zona central se marcan dos líneas a distancia L conocida entre las cuales se medirá la elongación de la barra mediante deformómetro mecánico o un instrumento electrónico muy sensible llamado LVDT (Low Voltage-Displacement Transducer).
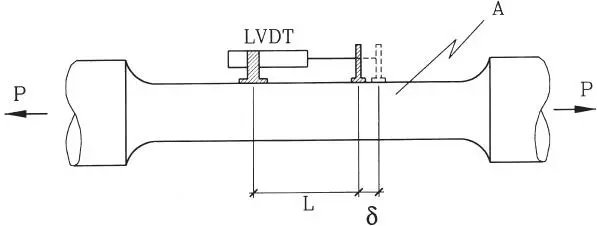
Figura 1.12Esquema del ensayo de tracción uniaxial
El ensayo consiste en aplicar una deformación axial a la probeta de modo de aumentar P desde cero hasta la ruptura de la barra, leyendo para cada valor de P la elongación d y calculando la tensión σ = P/A, en que A es el área inicial de la sección, y la deformación unitaria ε = δ/L, las que se grafican resultando un gráfico como el siguiente:
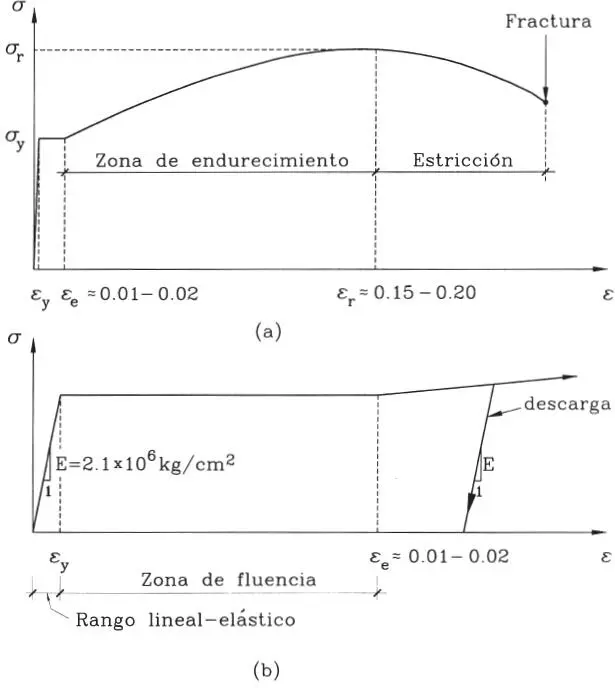
Figura 1.13Relación tensión-deformación del acero estructural
En este gráfico se distinguen tres fases de comportamiento del acero estructural:
• El rango llamado lineal-elástico en que se cumple la ley de Hooke, esto es, tensiones y deformaciones unitarias son directamente proporcionales, y las deformaciones son recuperables, es decir, desaparecen una vez removida la carga.
Читать дальше



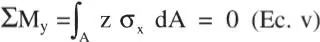
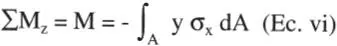
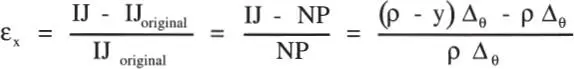
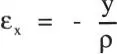
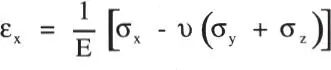
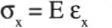
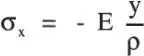
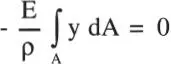
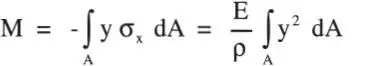
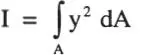
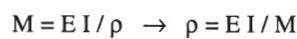
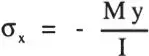
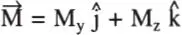 (Fig. 1.11). Se obtiene (Crandall y Dahl, 1972):
(Fig. 1.11). Se obtiene (Crandall y Dahl, 1972):













