Rafael Riddell C. - Diseño estructural

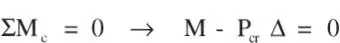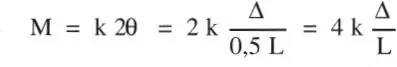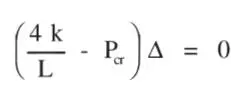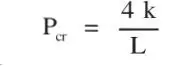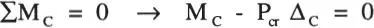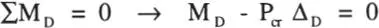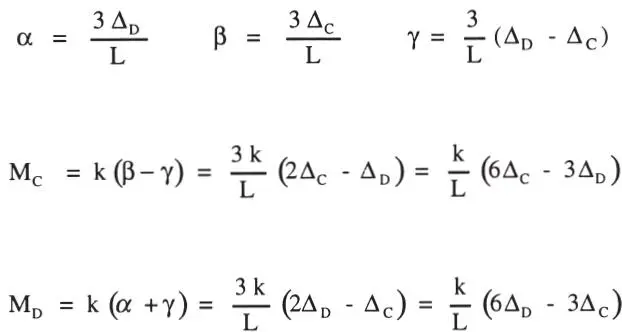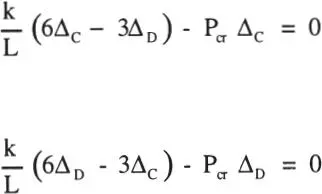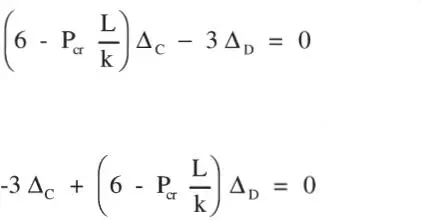
Figura 1.24Concepto de rigidez

Es claro para el resorte de la Fig. 1.22.c que δ = fF, pudiéndose constatar que mientras más flexible es un sistema, es decir, mientras mayor es f, mayores son las deformaciones (δ) para la misma fuerza constante (F). Lo mismo se puede extender a los ejemplos de las Figs. 1.22.d a 1.22.f; en esta última figura la relación entre fuerzas y deformaciones queda {δ}=[f][F], en que [f]=[k] -1se denomina matriz de flexibilidad . Sus coeficientes son constantes en un estructura linealelástica.

El cuarto y último concepto a destacar es el de ductilidad y su antónimo (no inverso) la fragilidad . Como se definió en su oportunidad la ductilidad es la capacidad de desarrollar grandes deformaciones plásticas, como el acero estructural, mientras la fragilidad es la incapacidad de hacerlo como ocurre con el hormigón o la madera.

1.2.3 Inestabilidad Estructural

Se ha mencionado en la Sección 1.1.3 que el proceso de diseño estructural involucra examinar el nivel de tensiones que se produce en las diferentes secciones de los elementos, y verificar que las deformaciones de estos elementos no superen ciertos límites fijados por condiciones de serviciabilidad. Sin embargo, el diseño de elementos o estructuras esbeltas implica, además, el asegurarse que no se producirá una falla por inestabilidad. Este es un tipo de falla diferente a los analizados anteriormente, ya que se produce cuando se alcanza la carga última por inestabilidad, sin aviso previo de problemas en el elemento o estructura, y para un nivel de tensiones que puede estar dentro de los límites aceptables de acuerdo al criterio de diseño por seguridad que se esté usando.

Para entender este fenómeno, se supondrá una columna formada por dos tramos rígidos unidos por un resorte de flexión de constante k, sometida a una fuerza de compresión axial P, tal como se indica en la Fig. 1.25.a. Si la carga Pes pequeña, al aplicar y retirar una fuerza horizontal F, la columna se deformará y volverá posteriormente a su posición inicial (Fig. 1.25.b), si la carga P es grande, la aplicación de la fuerza F hará que la deformación crezca indefinidamente, evidenciando la inestabilidad del sistema, y no vuelva a su posición inicial cuando F se haga cero (Fig. 1.25.c). Para un cierto valor intermedio de P, llamado carga crítica P cr, al aplicar F la columna se deforma, pero al hacer F = 0 la columna permanece en su posición deformada (Fig. 1.25.d). La carga crítica P cres la que delimita las condiciones de estabilidad e inestabilidad del sistema, y constituye la carga axial última para la falla por inestabilidad. Su determinación está dada por la posibilidad de encontrar posiciones deformadas de la columna, diferentes de la posición vertical, cuando actúa la carga crítica, tal como se detalla a continuación.

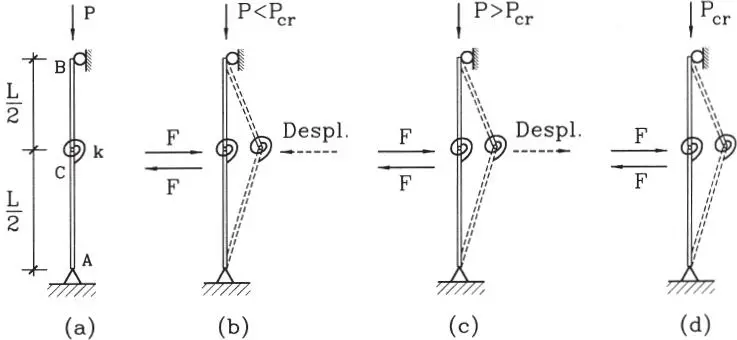
Figura 1.25Carga crítica de una columna

En la práctica, la acción de la fuerza F es reemplazada por imperfecciones de construcciones, excentricidades o imperfecciones respecto de la situación ideal. Asimismo, el caso ideal que se ha presentado cambia al caso de una columna flexible con rigidez a giros por flexión en toda su longitud. Este caso se discute en la Sección 2.3, pero los principios básicos para la determinación de la carga crítica son los mismos de este caso.

Se trata de encontrar el valor de P para el cual es posible encontrar un valor del desplazamiento Δ distinto de cero (Fig. 1.26). Por equilibrio de la parte superior de la columna se tiene:

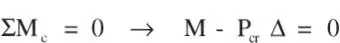
ya que por equilibrio general de la columna, la reacción horizontal H es nula; pero:

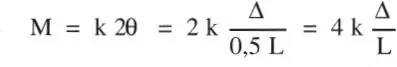
luego:

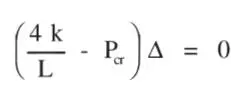
Esta ecuación, típica de un problema de inestabilidad, recibe el nombre de ecuación característica . Para deformadas con Δ distinto de cero, la única solución es:

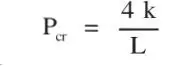
con lo que se obtiene el valor de la carga crítica. Si Pes distinto de Por, la ecuación no se satisface para valores de Δ diferentes de cero. Al mismo tiempo, el valor de Δ no es único cuando P= P cr, o sea, cualquier deformación Δ de la columna es posible. Todos estos aspectos caracterizan el problema de inestabilidad estructural o pandeo, el cual es muy diferente de los problemas de análisis de tensiones o deformaciones, que pueden calificarse como problemas de “respuesta”, esto es, hay un valor de la tensión o de la deformación para cada valor de la solicitación.

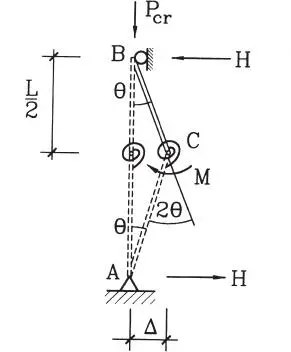
Figura 1.26Determinación de la carga crítica

En el Ejemplo 1.6 se ilustra un caso de inestabilidad con más de un parámetro para definir la posición deformada de la estructura.

Ejemplo 1.6

Determinar la carga crítica del sistema estructural de la Fig. E1.6.a.

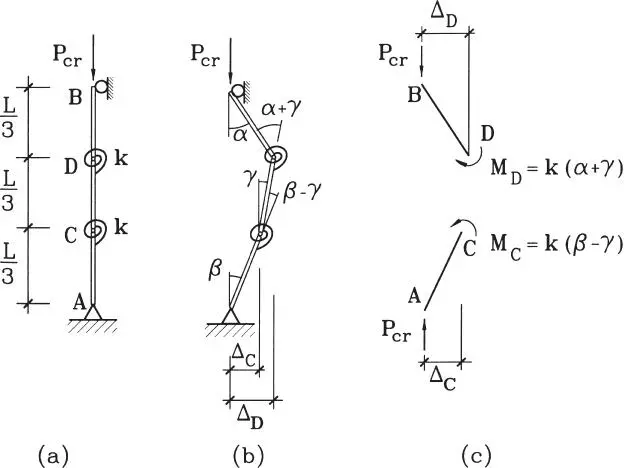
Figura E1.6

Solución:En este caso, la deformada del sistema está definida por los parámetros Δ Dy Δ C. Se busca la carga P para la cual es posible una deformada con Δ Dy/o Δ Cdistintos de cero. Tal deformada se muestra en la Fig. E1.6.b.

Equilibrio de AC:

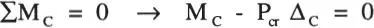
Equilibrio de BD:

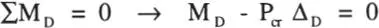
Pero, considerando deformaciones pequeñas:

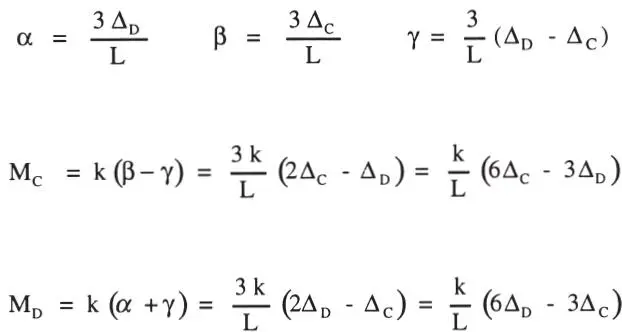
y reemplazando en las ecuaciones de equilibrio, se tiene:

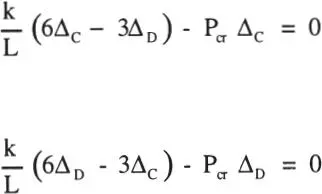
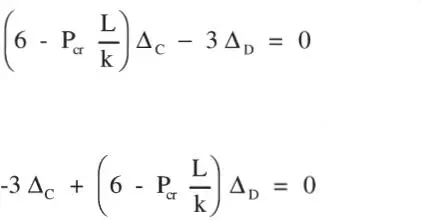
Para que existan soluciones Δ Cy Δ Ddistintas de cero, se requiere que: