Understanding the growth mechanisms of species continues to occupy scientists. In the first half of the 20th Century, the British biologist d’Arcy Thompson (1881–1946) became interested in the shape and growth of living organisms, publishing his thoughts in an exciting collection [THO 61]. He looks for invariants and universal principles that govern the evolution of life – for example, fractal structures or particular sequences (Figure 1.20).

Figure 1.20. The Fibonacci spiral: a model (too simple?) to explain plant growth
(source: www.123rf)
COMMENT ON FIGURE 1.20.– Leonardo Fibonacci (1170–1250) was a 13th Century Italian mathematician. The Italy of his time was a region formed by scatterings of merchant cities in strong competition (Venice, Pisa, Genoa). Trade activities needed numbers and calculation to support their economic development. The mathematician developed algebraic methods to contribute to this. In particular, he drew inspiration from Indian and Arab mathematics, while Roman numerals, still widely used in Europe, forced calculation in a rigid numbering system that the invention of zero helped to loosen. The sequence that bears his name is defined from two values, then each term is calculated as the sum of the two previous ones. Thus, starting from 1 and 1, the terms are 2, 3, 5, 8, 13, 21, etc. This sequence, which has properties of interest to mathematicians, is found in some natural growth mechanisms. The Fibonacci sequence hides the famous golden number 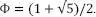 Discovered in the 3rd Century BC by Greek mathematicians , Φ seems to be present behind the architectural choices made in antiquity, for example in the construction of the Parthenon in Greece. “Let no one ignorant of geometry enter” is the motto of the Academy, founded in Athens by Plato in the 4th Century BC. The Platonic school makes mathematics one of the instruments of the search for truth. To this is added that of harmony, whose golden number is the hyphen . Φ is the Greek letter traditionally used to designate it and it also refers to philosophy. For very different reasons, the golden number fascinates human beings who sometimes tend to find it everywhere even where it is not [LIV 02] .
Discovered in the 3rd Century BC by Greek mathematicians , Φ seems to be present behind the architectural choices made in antiquity, for example in the construction of the Parthenon in Greece. “Let no one ignorant of geometry enter” is the motto of the Academy, founded in Athens by Plato in the 4th Century BC. The Platonic school makes mathematics one of the instruments of the search for truth. To this is added that of harmony, whose golden number is the hyphen . Φ is the Greek letter traditionally used to designate it and it also refers to philosophy. For very different reasons, the golden number fascinates human beings who sometimes tend to find it everywhere even where it is not [LIV 02] .
Created at the initiative of the Royal Botanical Garden of Edinburgh, the website The Plant List3 aims to provide an exhaustive list of the various plant species: there are currently more than 1 million. Nature is characterized by a great variability of shapes (Figure 1.21): how can we accurately model the development of such diverse plants?

Figure 1.21. Variety of leaf shapes
(source: www.123rf/Liliia Khuzhakhmetova)
Since the late 1960s, scientists have been using a formalism that is particularly well suited to modeling plant growth. It finds its roots not in the field of mathematics but in that of grammar! Frédéric Boudon, a researcher at CIRAD* , is an expert in these tools, the so-called “L-systems”:
“The L-systems were introduced in the late 1960s by Hungarian biologist Aristid Lindenmayer to describe some of the processes encountered in biology. They are particularly effective in modeling plant development and are based on the rules of ‘formal grammar’. These can provide a realistic account of the influence of the plant’s architecture, vitality and environment on its growth”.
In an L-system, a plant is represented by a sentence whose elements, or modules, themselves symbolize the components of the plant (stem, branch, flower, leaf, etc.). A set of rules governs the dynamics of these modules: they formalize biological processes and model plant transformations. The production of a new element (leaf, flower, fruit), growth or division of an existing element (stem, branch) are therefore represented by sentence equivalents of our language, which itself has its own syntactic rules (the order of words in a sentence) and is based on a given semantics (a set of words).

Figure 1.22. Weeds generated by a three-dimensional L-system program
(source: www.commons.wikimedia.org )
COMMENT ON FIGURE 1.22.– The rules implemented in the L-systems seek to represent the living: the probability of regrowth of a cut part, the amount of biomass produced, the birth and hatching of a flower, the production and ripening of a fruit. They can take into account environmental factors: amount of light received, level of sugar reserves, concentration of a hormone, etc. They make it possible to arrive at a very realistic modeling, a genuine digital plant!
“The validation of models is done by comparing them with the dynamics and patterns observed in the field. There are no specific restrictions on the use of L-systems and researchers can therefore treat any type of plant: grasses, plants, trees! Their architectures can be reproduced in a very realistic way, including at fine detail levels. By using so-called ‘stochastic approaches’, it is possible to reproduce by simulation the heterogeneity observed in nature. Different biophysical phenomena such as branch mechanics or their reorientation towards the sun or as a function of gravity can be included in these simulations”.
While they formalize the understanding of plant growth through simple mathematical rules, L-system-based models allow different types of applications such as yield prediction. The challenge in this case is to have models interact at different scales in order to obtain an overview: from plants or planting groups, to the plot and the entire farm. This is a vast field of research in digital agriculture. Modeling by L-systems already contributes to the evaluation of certain techniques, such as agro-ecology, which are receiving increasing interest due to the growing awareness of ecological issues and the need to preserve the emerald forest?
NOTE.– Growing plants “in-silico” with L-systems .
The typology of a plant, the phenotype, results from the expression of its genetic heritage (its genotype), and its interactions with the characteristics of the environment in which it develops (its environment). These interactions largely determine biomass production: reconstituting the phenotype of plants is therefore a key-factor in calculating the yield of a production.
Artificial intelligence techniques based on deep learning from imaging data can contribute to this objective by automatically and quickly performing repetitive tasks such as counting sheets. In the learning phase, it is necessary to have a database large enough to make the algorithms efficient, which is not always the case in agronomy! The databases that can be used are generally limited and campaigns to enrich them are very expensive. One solution proposed by some researchers is to generate digital plants by simulation: the variety of forms produced thus enriches existing databases at low cost (Figure 1.23).

Figure 1.23.The virtual plants (left), obtained in silico by means of L-systems, have similar characteristics to the real plants (right), obtained in vitro
Читать дальше


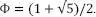 Discovered in the 3rd Century BC by Greek mathematicians , Φ seems to be present behind the architectural choices made in antiquity, for example in the construction of the Parthenon in Greece. “Let no one ignorant of geometry enter” is the motto of the Academy, founded in Athens by Plato in the 4th Century BC. The Platonic school makes mathematics one of the instruments of the search for truth. To this is added that of harmony, whose golden number is the hyphen . Φ is the Greek letter traditionally used to designate it and it also refers to philosophy. For very different reasons, the golden number fascinates human beings who sometimes tend to find it everywhere even where it is not [LIV 02] .
Discovered in the 3rd Century BC by Greek mathematicians , Φ seems to be present behind the architectural choices made in antiquity, for example in the construction of the Parthenon in Greece. “Let no one ignorant of geometry enter” is the motto of the Academy, founded in Athens by Plato in the 4th Century BC. The Platonic school makes mathematics one of the instruments of the search for truth. To this is added that of harmony, whose golden number is the hyphen . Φ is the Greek letter traditionally used to designate it and it also refers to philosophy. For very different reasons, the golden number fascinates human beings who sometimes tend to find it everywhere even where it is not [LIV 02] .













