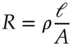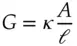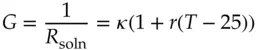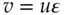Gary A. Mabbott - Electroanalytical Chemistry

Electrical conductance is a measure of the ability to carry current. Resistance is defined as the reciprocal of conductance. It is easily measurable. Because the measurement of the resistance of a solution depends on the area of the electrodes and the distance separating them, the standard method uses two square platinum plates, 1 cm on each edge separated by 1 cm of solution (see Figure 1.11).

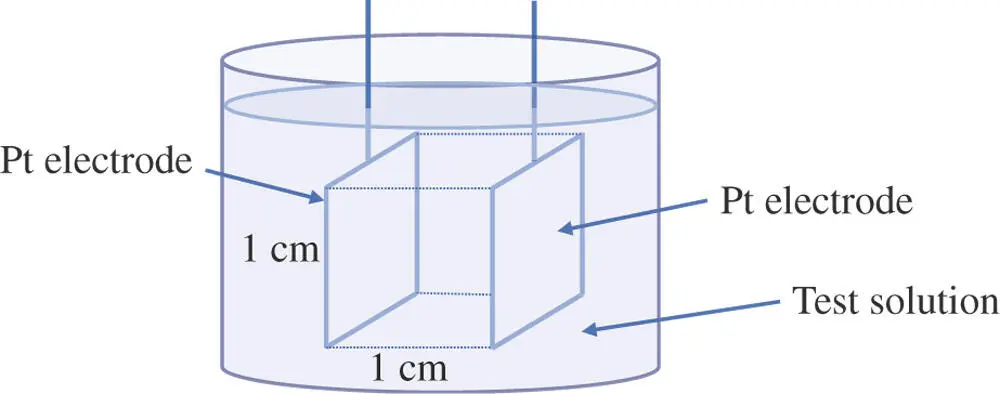
Figure 1.11Conductance cell.

Of course, the interface between the solution and each plate develops an electrical double layer. As a consequence, the electrochemical cell behaves as a circuit with two capacitors in addition to the solution resistance. The resistance is measured using a special meter that applies an oscillating voltage to the electrodes and measures the current response. The resistance component has to be extracted from the response. The resulting resistance is called the specific resistance of the solution, ρ , and has the units of Ω cm. The electrical resistance for any other arrangement of electrodes is proportional to the length, ℓ , of solution between the electrodes of area, A .

(1.26)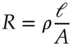

where ρ is the proportionality constant. Because conductance is inversely related to resistance one can define the conductance, G in Siemens, as follows:

(1.27)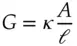

where κ is the electrical conductivity of the solution in units of Ω −1cm −1or S cm −1. Although the standard method defines the shape and separation for electrodes, commercial instruments often have a different geometry and correct for differences by applying a calibration factor.

The solution resistance and conductance also varies with temperature [13].

(1.28)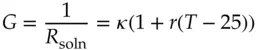

where T = the solution temperature in °C and r is a temperature coefficient in Siemens/degree for the solution. The temperature coefficient needs to be evaluated for different electrolyte solutions, but a representative value is r = 0.0191 for a 0.01 M KCl solution [13].

The conductance of a solution also depends on the type of ions that make up the electrolyte. The important point here is that ions move at different speeds. Ions move by diffusion, the process that is conceptualized as a random walk of individual particles, but under the influence of an electric field, they also migrate in the direction of the oppositely charged electrode. The velocity of an ion caused by an electric field is sometimes called the drift velocity or the migration velocity. It is proportional to the strength of the electric field, ε , driving the current.

(1.29)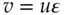

where the electric field, ε , has the units of V/cm. It is the voltage difference between the electrodes divided by the distance between them. v is the drift velocity of the ion in cm/s and the proportionality constant, u , is the ion mobility. The units for the ion mobility are cm 2/(s V). The reason that the mobilities vary among ions is the fact that collisions with solvent molecules and other particles cause drag. Drag is related to the size of the ion. In this context, the size of the ion includes the sheath of solvent molecules that the ion drags with it, its solvent sphere. The bigger the solvated ion, the greater the viscous drag force opposing the ion's movement. All ions are slowed down by the viscosity of the solution. Because the viscosity decreases with temperature, the conductance increases with temperature as indicated in Eq. (1.28). The ion mobility is also proportional to the charge on the ion. Also, the bigger the charge, the greater the tug that the electric field exerts on the ion. Each ion carries a fraction of the total current in proportion to its mobility and its contribution to the total number of charges in solution. An important consequence of the variation in ion mobilities is the fact that the current is shared unevenly among the ions.

There are two practical applications of conductance or conductivity measurements that are of interest to analytical chemists. The first application is a semiquantitative estimate of ion concentration. One can calibrate conductivity measurements for an accurate quantitative determination of a specific salt, if that is the only source of ions in the sample. However, such a situation constitutes a special case. In the area of environmental science and agriculture, conductivity measurements are often made as a general indicator of water purity. Conductivity is also a parameter that is monitored at the outlet of a water purifying system commonly used for analytical and biochemistry laboratories. The quality of the water is often described in terms of the specific resistance. Theoretically, the specific resistance of water with no ions other than those from the dissociation of water is 18.3 MΩ.

There is one common application where conductivity provides good data for quantitative determinations of specific ions. Conductivity detectors are very popular for ion chromatography. In this case, the conductivity cell has been miniaturized so that it can operate on volumes on the microliter scale. Ions eluting from the separation column flow through the electrochemical device and cause a surge in conductance in proportion to their concentration. A full discussion of how a conductivity detector works in liquid chromatography can be found elsewhere [14].

The movement of ions and molecules in solution is important in many different aspects of electrochemical analysis. The term “mass transport” is often used to mean that reactant material is being driven by some force to the surface of an electrode. The rate at which reactant material is brought to the electrode surface influences the sensitivity of methods in many cases. The two most common mass transport mechanisms are convection and diffusion. In the first case, the bulk solution is mechanically stirred or pushed past an electrode such as in a flowing stream. The term “hydrodynamic system” is also used to mean a flowing or stirred solution that continuously brings material to the electrode.

The other mechanism for mass transport that is exploited in electroanalysis is called diffusion. Diffusion moves material by the force of a concentration gradient. This mechanism is subtler and deserves some discussion here. Imagine two solutions separated by a square window, 1 cm on each edge (see Figure 1.12). Molecules move very rapidly at room temperature, but they are frequently colliding with each other and the solvent. Consequently, the path of any individual molecule changes direction many times per second. The molecule appears to be moving randomly. How fast it moves depends on its solvated radius. Imagine also that one can count the molecules that pass through the window in each direction. The net excess going one direction or the other per second is called the flux for that molecule. A flux has the same dimensions as the product of a concentration and a velocity. The normal units are mol/(cm 2s) (equivalent to mol/cm 3× cm/s). When the concentration for some molecule, M, on both sides of the window is equal, the number going from left to right through the window matches the number going from right to left each second. Consequently, the flux is zero.