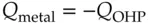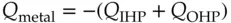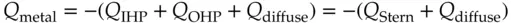Gary A. Mabbott - Electroanalytical Chemistry

(1.18)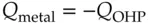

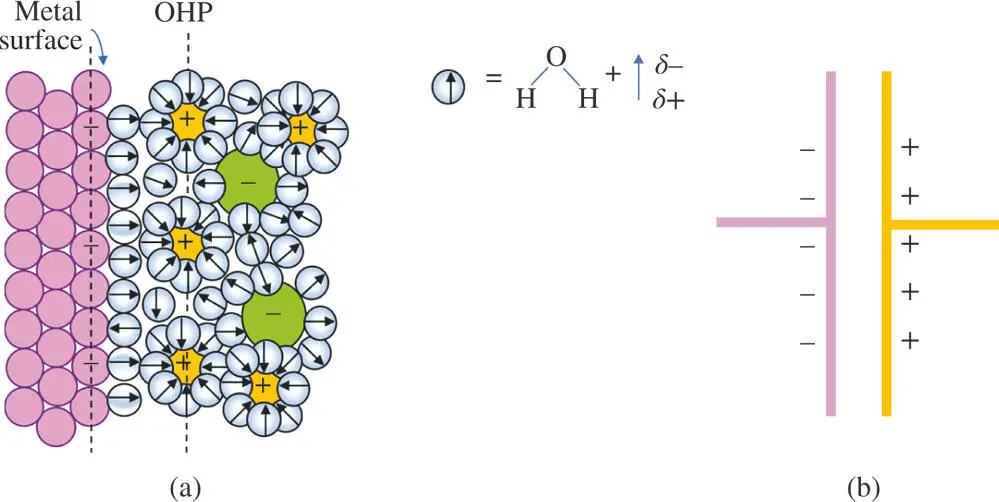
Figure 1.5The Helmholtz model of the electrified boundary between a metal surface (dark spheres) with a net negative charge and an aqueous salt solution. (a) Cations are attracted to the surface forming a net positive layer to balance the negative charge in the metal. Water molecules occupy the first layer on the metal surface. They also surround ions in solution aligning their dipoles according to the type of charge on the ion. (Arrows point toward the oxygen atoms.) The charges on the solution side define a layer called the outer Helmholtz plane (OHP) [5]. (b) The double layer of charge behaves like a capacitor producing an electrical potential energy difference between the two layers whose magnitude is proportional to the charge.

In cases where the solid surface has a net positive charge, it attracts an excess of anions to balance the charge and the OHP is occupied by an excess of anions. In some cases, individual anions are able to come into direct contact with the metal surface. This phenomenon is called contact adsorption. Whether or not contact adsorption occurs depends upon the net free energy for three separate steps in the overall adsorption process. Two of the steps are obviously endothermic. Removing water molecules from the electrode surface to make room for the anion and removing part of the hydration sphere around the ion both cost energy. Therefore, only interactions between the ion and the electrode surface that lead to strong bonds make the adsorption process favorable. The electrostatic attractions between oppositely charged ions and the electrode are not decisive by themselves. Contact adsorption relies on London dispersion forces, overlap of electron orbitals, and image forces. An image force is similar to the mechanism known as London dispersion forces where a momentary dipole resulting from the instantaneous arrangement of charge density around a molecule induces a rearrangement of electron density in a neighboring molecule creating a momentary dipole that results in dipole–dipole attraction. Unlike London dispersion forces, the image force is created by a permanent dipole or a charge on the ion inducing a dipole or local excess of charge in the electrode that leads to attraction at that location. The plane that includes the center of ions that are contact‐adsorbed to the electrode surface is often called the inner Helmholtz plane (IHP) (see Figure 1.6). An interesting consequence of these additional forces is that some anions can remain attached to the electrode surface even when the electrode is also negatively charged. To account for contact adsorption, the equation for the charge balance becomes

(1.19)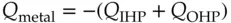

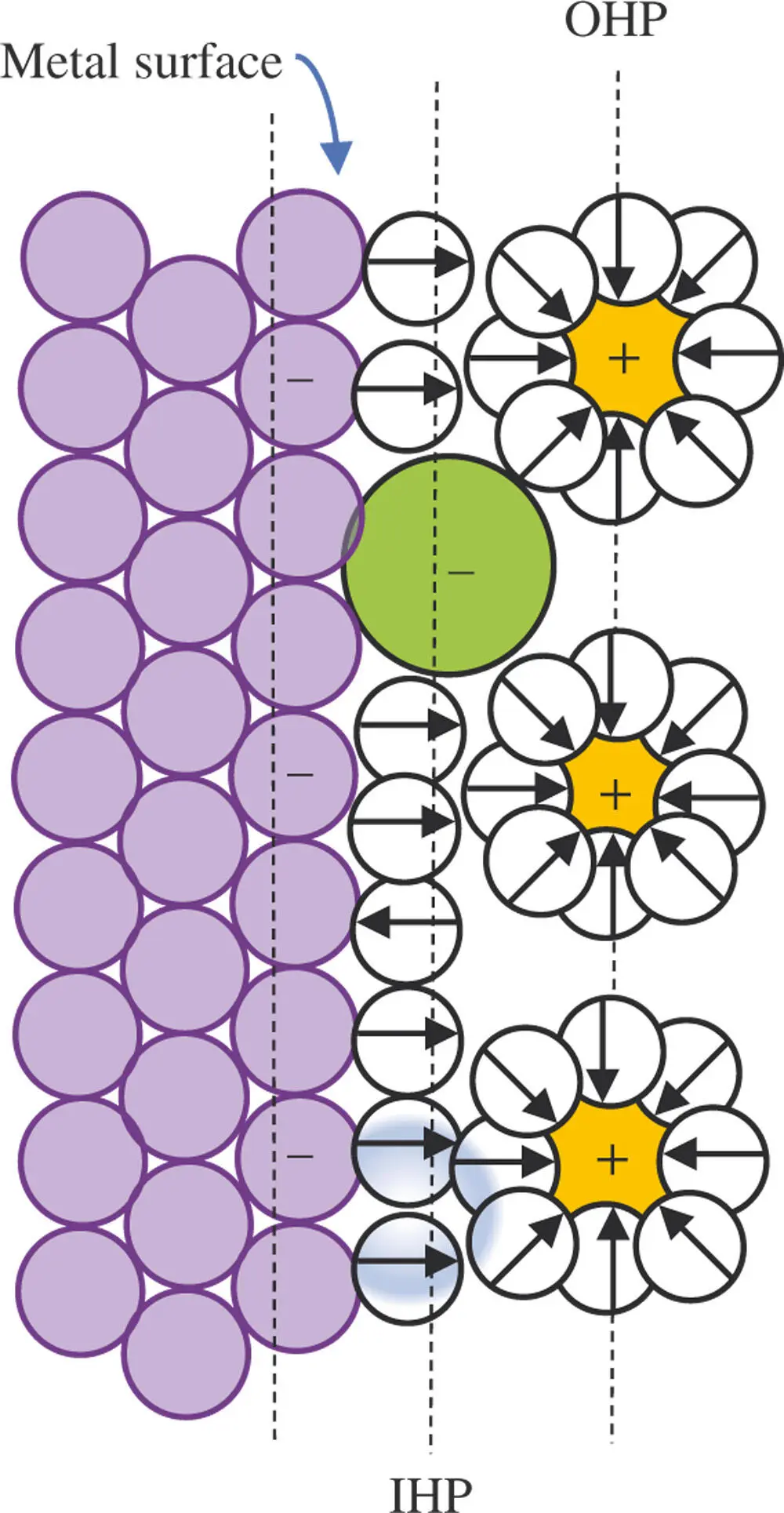
Figure 1.6The inner Helmholtz plane (IHP) is a plane parallel to the electrode drawn through the center of ions or neutral molecules adsorbed directly in contact with the electrode surface. London and image forces as well as electron overlap between the metal and ion are responsible for the net attraction. These forces can result in binding even when charge considerations oppose adsorption [5].

The model of Helmholtz suggests that all of the counter ions necessary to balance the charge on the electrode are held rigidly near the electrode surface. However, the experimental evidence suggests that thermal forces are great enough to dislocate counter ions to some degree. These observations inspired work by Louis Gouy [6] and by David Chapman [7] that led to a different model [5]. They proposed that the counter ions are distributed in a nonuniform manner with a high concentration of counter ions near the electrode that falls off exponentially with distance from the electrode surface (Figure 1.7).

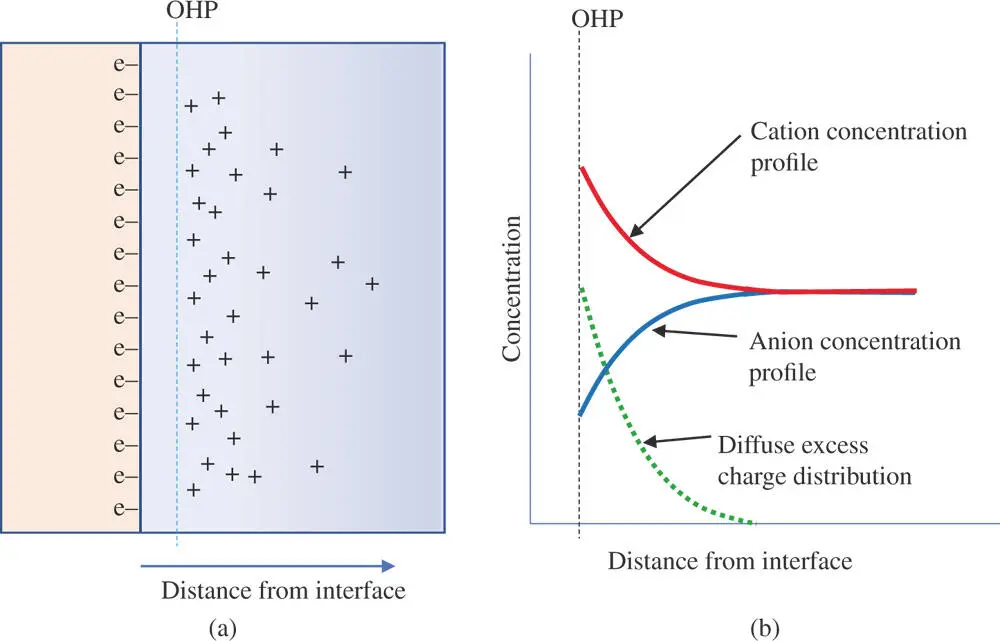
Figure 1.7(a) Gouy–Chapman model of electrical double layer showing a diffuse region of excess charge on the solution side. (Solvent molecules are not shown for clarity.) (b) The excess concentration drops off exponentially with distance from the electrode surface.

Unfortunately, this diffuse–charge model seemed to overcompensate. Experiments indicate that only a fraction of the charge appears to be disrupted by thermal agitation of the surrounding solution, whereas the diffuse charge model implied that it all was susceptible to thermal motion. In 1924, Otto Stern proposed a new model that was a synthesis of the earlier two [8]. Stern proposed that part of the compensating charge on the solution side is held tightly in the IHP plus the OHP and the remaining fraction of charge is contained in a diffuse zone of freely moving counter ions with a concentration that decreases with distance from the electrode surface. The IHP and OHP are sometimes collectively called the Stern layer. This layer is considered a stagnant zone of solution that clings to the surface. Figure 1.8shows the arrangement of ions at a negatively charged electrode according to the Stern model. The charge balance equation for the double layer becomes

(1.20)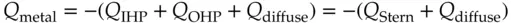

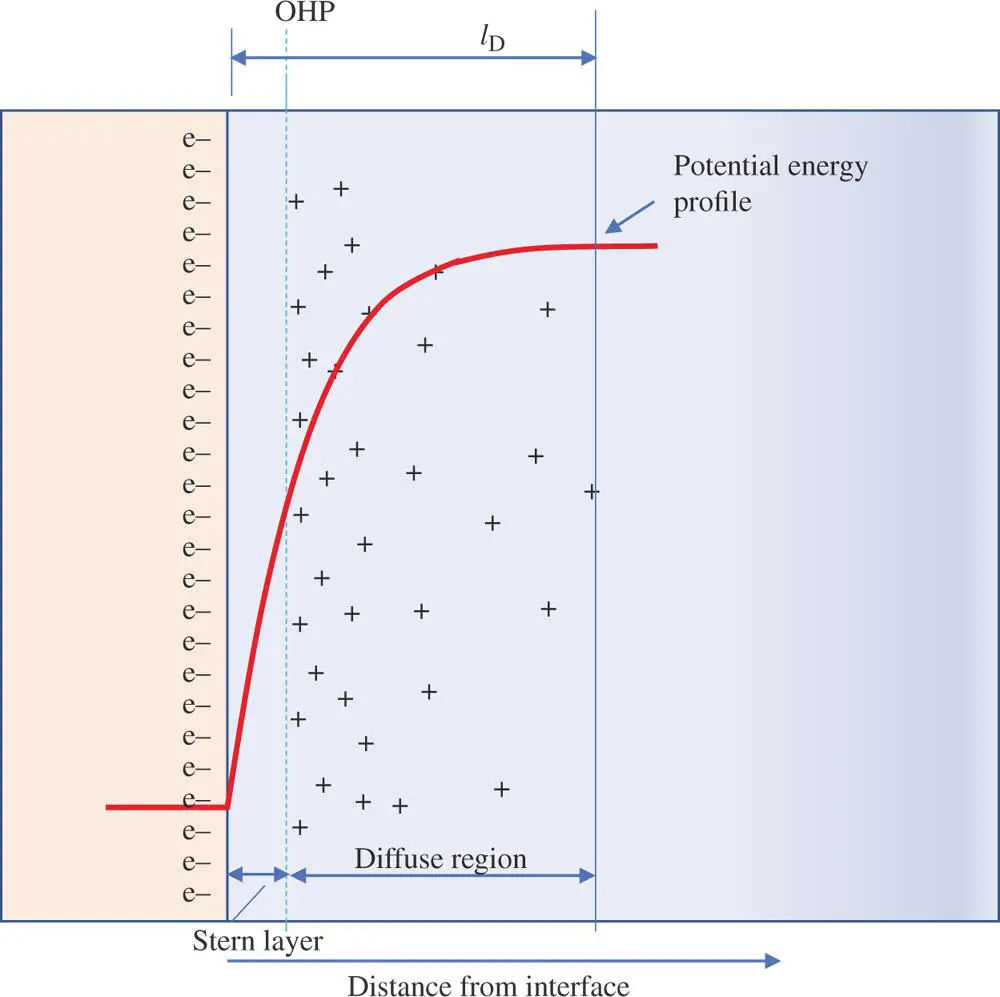
Figure 1.8Stern model of the electrical double layer. Charges and solvent at the OHP cling to the solid surface. Not all of the charge on the surface of the electrode is compensated by the excess of cations at the outer Helmholtz plane (OHP). A fraction of the counter charge is represented in a diffuse region just beyond the OHP. (Only the charges for the excess cations – the number of cations greater than the local number of anions – are pictured for clarity.)

Notice how the electrical potential changes as a function of distance from the electrode surface. The Stern model has several implications. One is that at higher electrolyte concentrations, the diffuse region of excess counter ions becomes more compact. The distance from the surface to the outer edge of the diffuse region is known as the Debye length, λ D. The Debye length is inversely proportional to the square root of the electrolyte concentration. A good benchmark to keep in mind is that the Debye length is about 100 Å (10 nm) for a sodium chloride solution of 0.01 M [9]. Most electroanalytical measurements are made at electrolyte concentrations of 0.01 M or higher. This profile for the potential has an important significance for voltammetry experiments where molecules must be transported to the electrode surface in order to exchange electrons with the surface. In most cases, the molecules can approach no closer than the OHP. Consequently, the electric potential that they experience is that of the OHP rather than the true potential of the electrode surface. As will be discussed in Chapter 5, this has important implications for the rate of electron transfer and the magnitude of the corresponding current in voltammetry experiments.