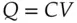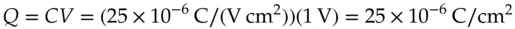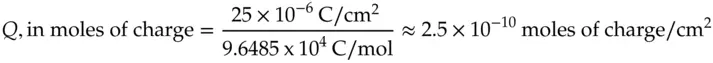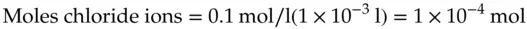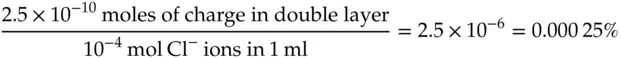Gary A. Mabbott - Electroanalytical Chemistry

It seems appropriate to pause here and note an application of electrochemical principles to phenomena outside of the field of electroanalysis. Naturally occurring phase boundaries involving electrified surfaces often occur in a variety of environments. Here is just one example in which the structure of the electrical double layer is especially relevant. River waters frequently carry tiny soil particles that remain suspended in the water because of the negative charges on the mineral surface (see Figure 1.9). These surface charges arise from the crystal structure in which some Al 3+and Si 4+ions are replaced by lower valence cations, such as Mg 2+. Cations from the surrounding solution form an electrical double layer with the surface of each clay platelet. In the river, where the electrolyte concentration is low, these charged particles have electrostatic fields that extend far enough into solution to keep neighboring particles from approaching each other closely. However, whenever a river flows into the sea, the ionic strength of the mixture increases suddenly (the sea is about 0.5 M in NaCl) decreasing the distance that the electrostatic field reaches from the surface of a particle. Under these conditions, collisions bring the particles close enough for attractive interactions, such as van der Waals forces and hydrogen bonding, to overcome the repulsion of the charges. The particles cling to each other and can settle out faster as a result.

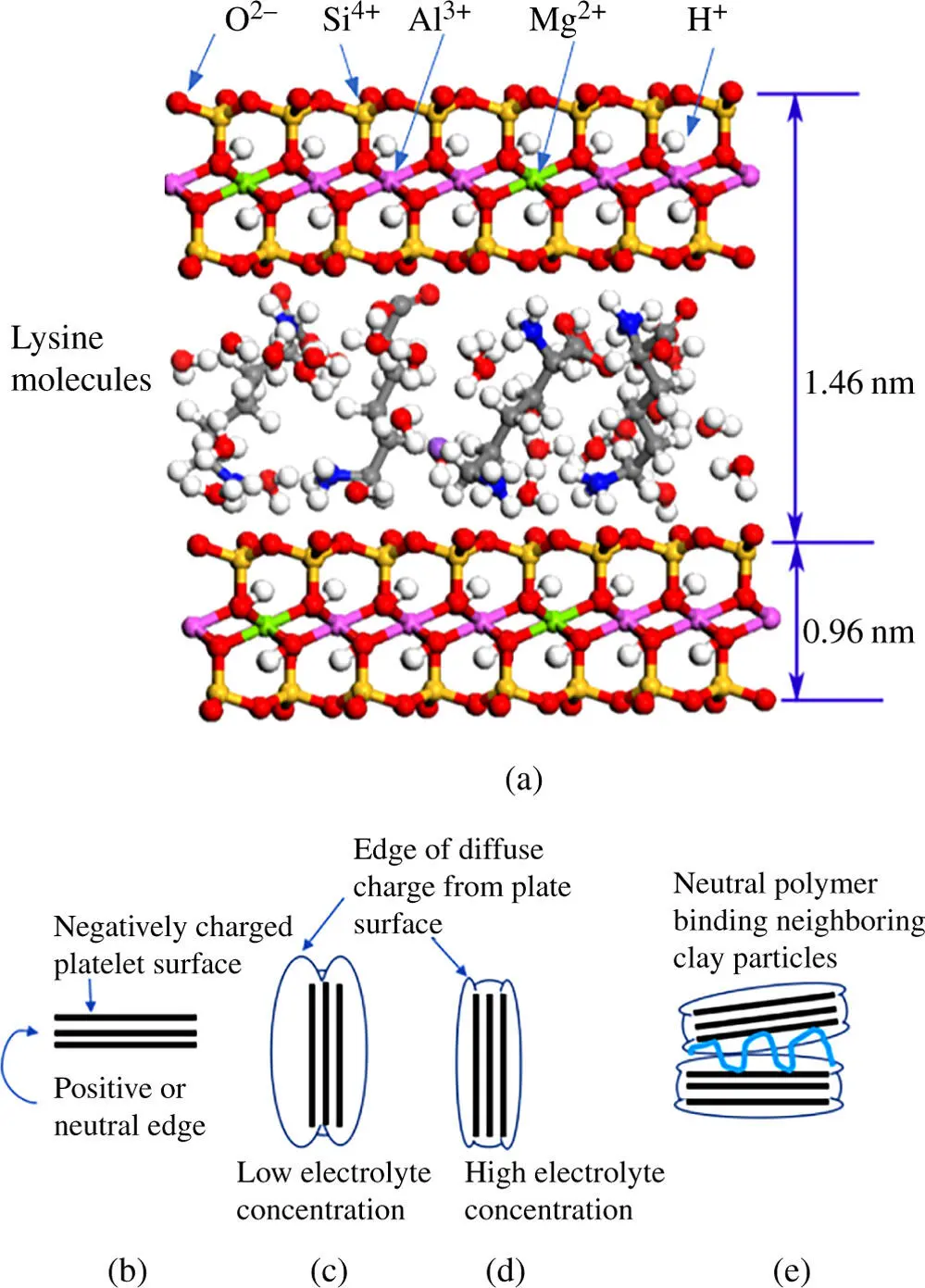
Figure 1.9The electrical double layer plays an important role in the suspension or sedimentation of tiny particles, such as clay platelets. (a) Montmorillonite clay mineral structure with lysine bridging plates. (b) The surfaces of clay platelets are negatively charged as a result of lower valence cations replacing Al 3+and Si 4+ions in the crystal lattice. (c) At low ionic concentrations, the diffuse charge region of the sides extends several nanometers out into solution effectively pushing neighboring particles apart. (d) At high electrolyte levels, the field from the diffuse part of the electric double layer compacts allowing clay particles to approach more closely [12]. (e) Neutral polymers, such as naturally occurring polysaccharides, can adsorb at multiple points to neighboring particles leading to aggregation. Aggregation processes are known as coagulation and flocculation.

Source: Adapted with permission from Zhu et al. [17]. Copyright 2019, Elsevier.

Seawater and soil particles are complicated mixtures and multiple mechanisms for binding particles together have been described. In some cases, calcium and other di‐ or tri‐valent cations can bridge between adjacent particles [10]. Another mechanism has been exploited in water treatment and industrial applications of clay materials. Water soluble, neutral polymers, such as polysaccharide chains, are added to clay suspensions in industrial processes to bridge between particles by hydrogen bonding to oxygen atoms in the clay surface [11]. Polymers that attach at several points but still loop out into the solution appear to work best. Presumably, the loops in the chains extend far enough to reach across the electric double layer of neighboring particles. The compression of the electrical double layer is a key part of the mechanism in both industrial and natural processes. As these particles agglomerate at the mouth of rivers, they settle out of solution‐carrying nutrients, and sometimes pollutants, into the sediments. This process has very important implications for the ecology of estuaries and the biological productivity of marine environments [12].

One can gain a lot of insight about electrochemical processes from approximating the behavior of an electrified interface with that of a capacitor. For example, it is interesting to think about how many charges are involved in creating a voltage across the boundary between two phases. An estimate can be made by modeling the electrical double layer as a simple capacitor where the solid metal constitutes one plate of the capacitor and the solution at the OHP (plus the diffuse region) serves as the second plate (Figure 1.10). (A similar argument can be made for other types of phase boundaries, such as between two ion‐containing liquids.)

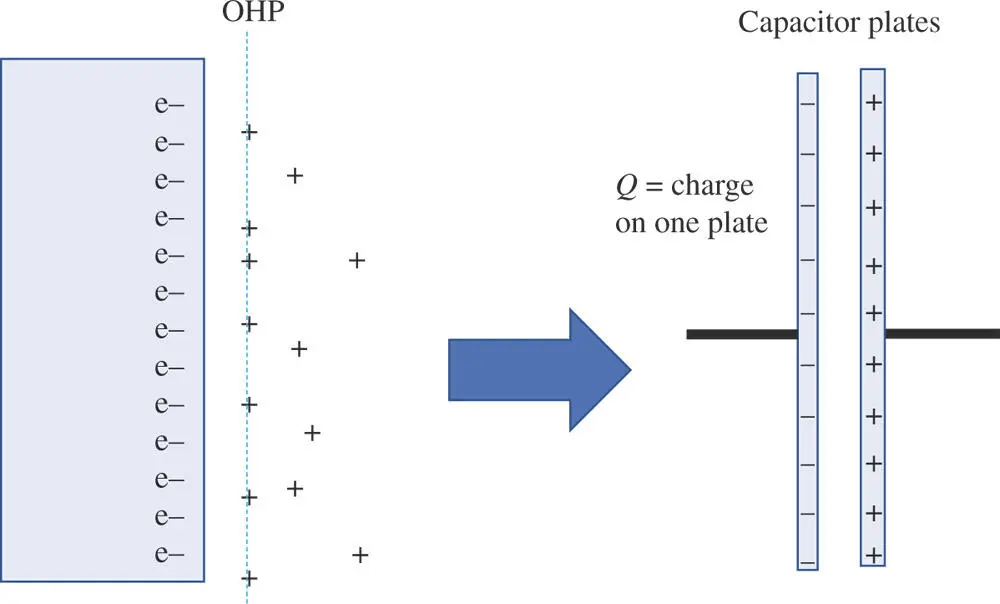
Figure 1.10The electrical double layer can be modeled as a capacitor where the charge Q is the charge on one plate.

Consider how much charge would be required to create an interface potential difference of 1.0 V. For the sake of discussion, consider a metal surface that has a net positive charge. The magnitude of charge, Q , that a capacitor accumulates on each side of the interface for a given voltage, V , separating the two plates is given by Eq. (1.21)[5].

( 1.21)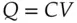

where the proportionality constant, C , is the capacitance of the dielectric medium separating the plates. (Here is the reason that the model is an over‐simplification. The double layer actually has a capacitance that varies with both the electrolyte concentration and with the double layer potential. However, this model does give results that set some upper limits. That is useful.) Empirically, the capacitance of the interface between a metal electrode in an aqueous salt solution is typically in the range of 10–40 μF/cm 2[9]. For convenience, a value at the midpoint of that range will be used, i.e. 25 μF/cm 2or 25 × 10 −6C/(V cm 2), to estimate the charge in this example. (Notice that the units on the value for the capacitance indicate that total charge depends on the electrode area.)

(1.22)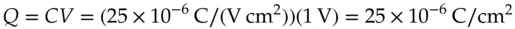

Because there are 9.6485 x 10 4C/mole of charge:

(1.23)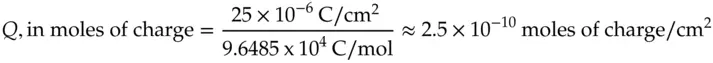

The calculation indicates that 2.5 × 10 −10mol of anions will be required to charge the double layer to a potential of 1.0 V. Thus, on a mole basis, the number of ions required to charge the solution side of the interface is tiny. For comparison, consider the number of moles of anions present next to a square electrode 1 cm on a side. Consider the chloride ions in a volume of 1 cm 3solution of 0.1 M NaCl.

(1.24)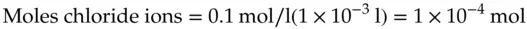

(1.25)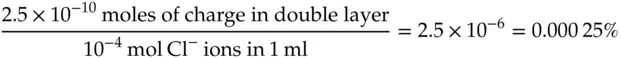

Charging the electrode to 1.0 V would require less than 0.0003% of the chloride ions from the surrounding milliliter of solution to be recruited into the double layer. Clearly, that amount represents a negligible loss to the Cl −concentration in the neighboring solution.

For every potential difference that appears across the double layer, there is a corresponding arrangement of charge. If the number of charges changes, the double layer potential changes. Likewise, if one is applying a voltage to the interface, then one must move electrons and ions to establish any new arrangement of charge. Because the movement of charge constitutes a current, then a current will exist until the new arrangement of charge is established. This phenomenon is called the double layer charging current. It can be a problem in some voltammetry experiments, because the signal current may be much smaller than the double layer charging current. In applied potential techniques one is usually interested in measuring the current that is related to the amount of analyte that is being oxidized or reduced at the electrode interface. The signal current associated with the oxidation or reduction of a chemical species is called a Faradaic current because the charge exchanged between the electrode and the electroactive species in solution is proportional to the number of moles of analyte that is oxidized or reduced according to Faraday's law ( Q = ∫ i d t = nFN ). The double layer charging current is non‐Faradaic; it represents a background component that one must remove from the signal in order to perform quantitative analyses. Methods for circumventing the double layer charging current are described in Chapter 5on controlled potential techniques.