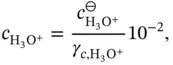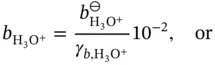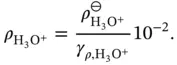Tarso B. Ledur Kist - Open and Toroidal Electrophoresis
Здесь есть возможность читать онлайн «Tarso B. Ledur Kist - Open and Toroidal Electrophoresis» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Open and Toroidal Electrophoresis
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Open and Toroidal Electrophoresis: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Open and Toroidal Electrophoresis»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
The exact expressions of separation efficiency, resolution, peak capacity, and many other performance indicators of the open and toroidal layouts are presented and compared.
Featuring numerous illustrations throughout,
offers chapters covering: Solvents and Buffer Solutions; Fundamentals of Electrophoresis; Open Layout; and Toroidal Layout. Confronting Performance Indicators is next, followed by chapters on High Voltage Modules and Distributors; Heat Removal and Temperature Control; and Detectors. The book finishes with an examination of the applications of Toroidal Electrophoresis.
The first book to offer a detailed account of Toroidal Electrophoresis—written by one of its creators
Compares the toroidal layouts with the well-established open layouts of the three most used platforms (Capillary, Microchip, and Slab) Provides solutions to many of the experimental issues arising in electromigration techniques and discusses the voltage distributors and detectors that are compatible with the toroidal layouts Richly illustrated with a large number of useful equations showing the relationships between important operational parameters and the performance indicators
is aimed at method developers and separation scientists working in clinical analysis, and food analysis, as well as those in pharmacology, disease biomarker applications, and nucleic acid analysis using the Capillary, Microchip, or slab Platform. It will also benefit undergraduate and graduate students of inorganic analytical chemistry, organic analytical chemistry, bioanalysis, pharmaceutical sciences, clinical sciences, and food analysis.

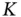 and
and 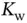 of water can be written as:
of water can be written as: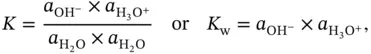
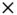 to avoid confusion,
to avoid confusion, 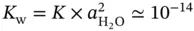 at 25
at 25 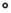 C and
C and 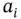 represents dimensionless variables called chemical activities. The activity
represents dimensionless variables called chemical activities. The activity 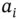 of a chemical species
of a chemical species 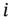 is defined as:
is defined as: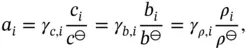
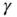 is a dimensionless parameter called the activity coefficient , which depends on the units of concentration of the variables
is a dimensionless parameter called the activity coefficient , which depends on the units of concentration of the variables 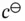 ,
, 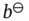 , and
, and 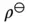 . These are standard states of solute concentrations with the following units, respectively: amount concentration (molar), molality (molal), and mass concentration (g
. These are standard states of solute concentrations with the following units, respectively: amount concentration (molar), molality (molal), and mass concentration (g 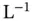 ). They should not be confused with the standard solutions used in analytical chemistry, nor with the standard conditions of a system (e.g., standard temperature and pressure of a gas). These standard states are standard quantities of a thermodynamic variable and in the present case could be 1 M, 1 molal, and 1 g L −1.
). They should not be confused with the standard solutions used in analytical chemistry, nor with the standard conditions of a system (e.g., standard temperature and pressure of a gas). These standard states are standard quantities of a thermodynamic variable and in the present case could be 1 M, 1 molal, and 1 g L −1.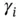 of a chemical species
of a chemical species 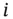 is close to one for a given range of concentration amount or other unit, then this species exhibits an almost ideal behavior according to Henry's law in this range and the same is expected up to infinite dilutions of the solute.
is close to one for a given range of concentration amount or other unit, then this species exhibits an almost ideal behavior according to Henry's law in this range and the same is expected up to infinite dilutions of the solute.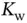 is called the autoprotolysis constant , [7] the water dissociation constant, the ionization constant or self-ionization constant of water. From the definition shown in equation 1.9it may also be seen as the ionic product of water . These are small numbers that are difficult to handle. Therefore it is more practical to apply the mathematical operator “p”, which stands for “
is called the autoprotolysis constant , [7] the water dissociation constant, the ionization constant or self-ionization constant of water. From the definition shown in equation 1.9it may also be seen as the ionic product of water . These are small numbers that are difficult to handle. Therefore it is more practical to apply the mathematical operator “p”, which stands for “ 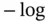 ”, to them. Consequently we obtain:
”, to them. Consequently we obtain: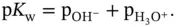
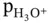 and
and  , respectively. For all other entities the notation
, respectively. For all other entities the notation 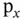 , where
, where 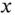 denotes any charged or neutral species, is used. For example,
denotes any charged or neutral species, is used. For example, 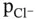 ,
, 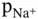 ,
, 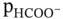 ,
, 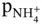 ,…, and so on.
,…, and so on.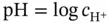 or
or 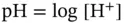 , because the transcendental functions (exponential, logarithmic, and trigonometric) must be handled with dimensionless arguments. Second, from a chemical point of view, the cited expressions are not very informative. To illustrate this, let us suppose that the pH of a solution is exactly
, because the transcendental functions (exponential, logarithmic, and trigonometric) must be handled with dimensionless arguments. Second, from a chemical point of view, the cited expressions are not very informative. To illustrate this, let us suppose that the pH of a solution is exactly 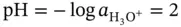 . From equation 1.10we can see that this is much more information rich, as it leads to the following relationships:
. From equation 1.10we can see that this is much more information rich, as it leads to the following relationships: