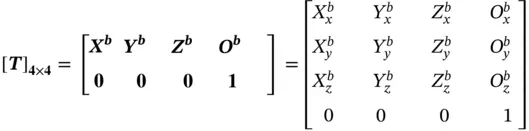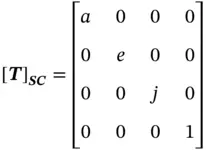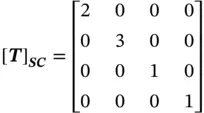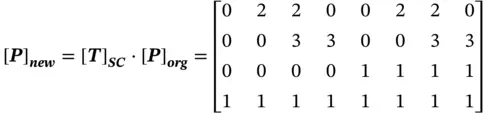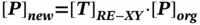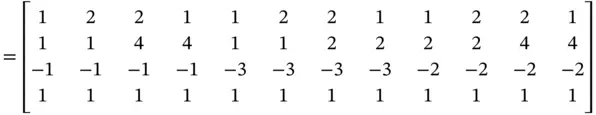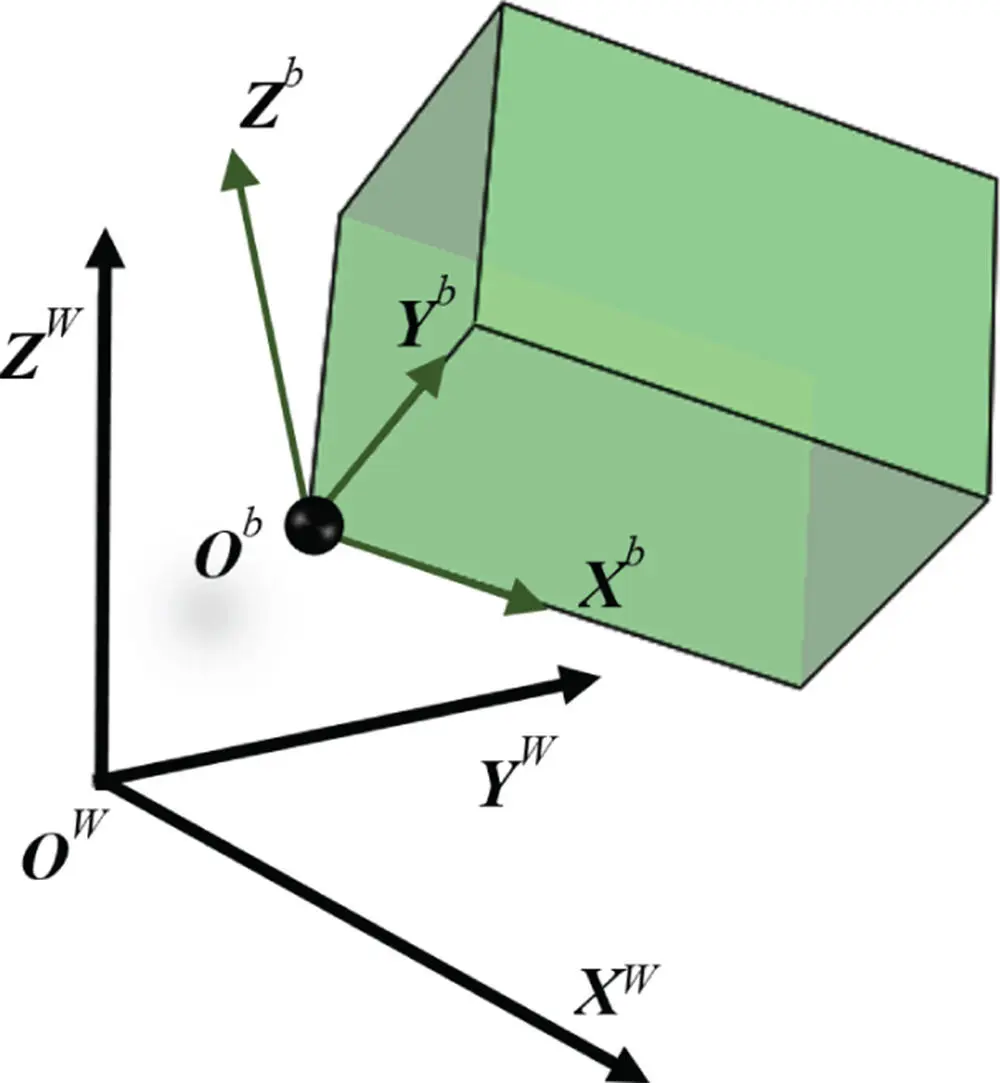
Figure 2.9Object coordinate system in a world coordinate system.
In Figure 2.9, a reference origin 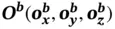 is used to represent the position of the object with respect to the world coordinate system ( O w− X w Y w Z w) and the orientation of the object is represented by three unit vectors ( X b, Y b, Z b). Furthermore, a homogeneous coordinate ( x , y , z , h ) and the corresponding 4 by 4 homogenous matrix [ T] 4x4in Eq. (2.4) are widely used to facilitate the matrix manipulations for the coordinate transformation of objects:
is used to represent the position of the object with respect to the world coordinate system ( O w− X w Y w Z w) and the orientation of the object is represented by three unit vectors ( X b, Y b, Z b). Furthermore, a homogeneous coordinate ( x , y , z , h ) and the corresponding 4 by 4 homogenous matrix [ T] 4x4in Eq. (2.4) are widely used to facilitate the matrix manipulations for the coordinate transformation of objects:
(2.4) 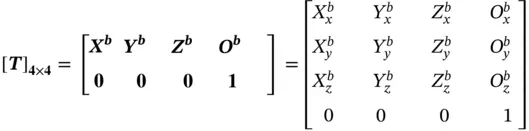
where [ T] 4 × 4is the homogenous matrix for the representation of an object CS { O b− X b Y b Z b} in the world coordinate system ( O w− X w Y w Z w).
Note that the homogenous matrix in Eq. (2.4) includes six independent variables: three for the position and the rest for the orientation.
A homogenous transformation matrix can be generalized to deal with any transformation of objects in a coordinate system. Figure 2.10shows the generalized matrix of homogeneous transformation. The elements of the matrix in different fields affect the transformation of an object in different ways. For examples, the elements ( a , e , j ) scale the coordinates of x , y , and z , the elements ( p , q , r ) translate the coordinates of x , y , and z , and the element s gives an overall inverse scale of the object.
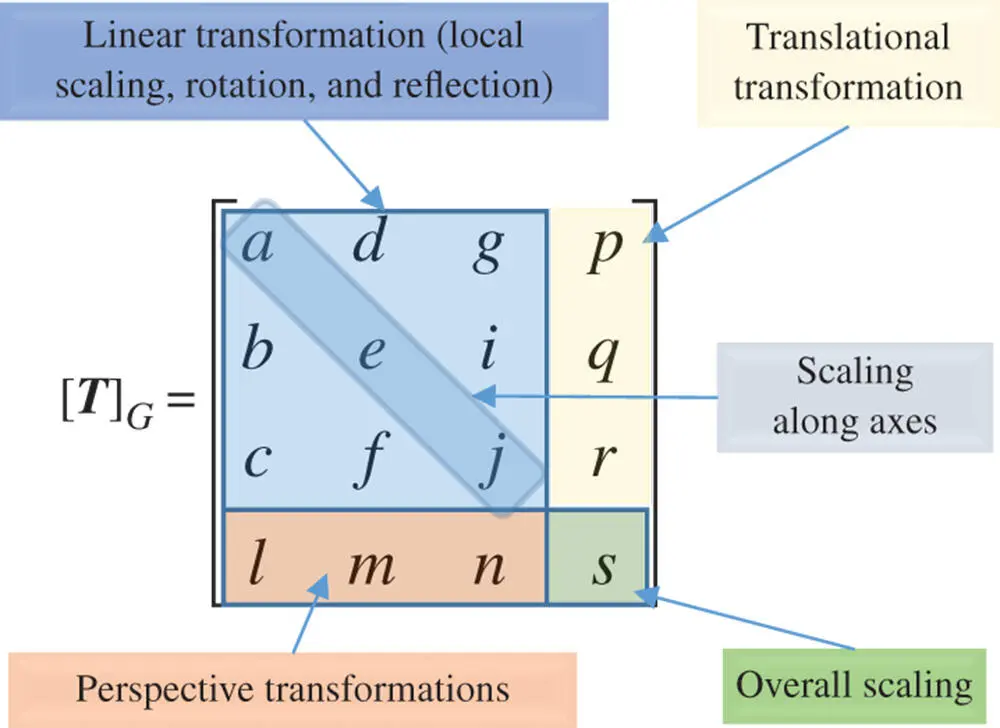
Figure 2.10Impacts of elements in a generalized homogeneous matrix.
The generic homogeneous matrix [ T] Gcan be customized to implement some common coordinate transformations of an object. For example, the translation matrix [ T] TRof an object can be simplified as
(2.5) 
where [ T] TRis the 3D translation matrix and p , q , r are the translational distances of a point from its original position along the x, y, and zaxes, respectively.
The scaling matrix [ T] SCof a 3D object can be defined as
(2.6) 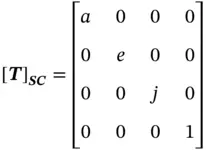
where [ T] SCis the 3D scaling matrix and a , e , j are the scaling factors along the x, y, and zaxes, respectively.
Given a cube with the size of 1 × 1 × 1 at its origin in Figure 2.11, determine the vertices of the object after the lengths along the x, y, zaxes are scaled up by 2, 3, and 1, respectively.
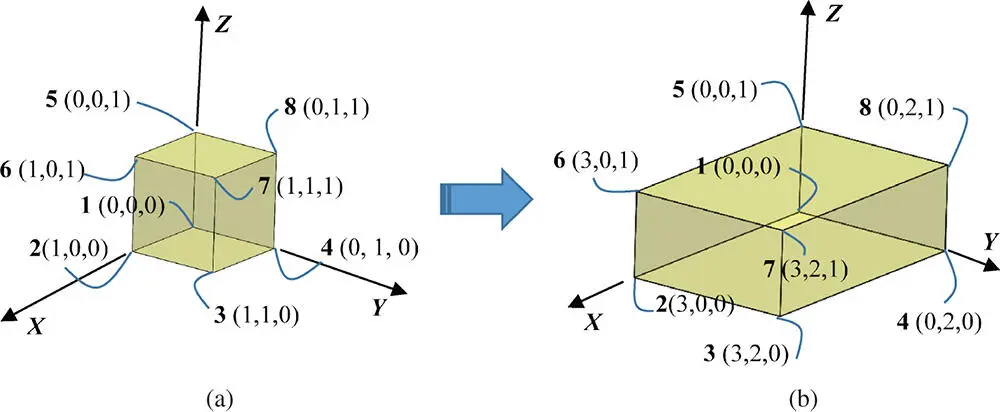
Figure 2.11Example of a scaling matrix of a 3D object. (a) Before transformation. (b) After transformation.
Before the transformation, the set of eight vertices (1, 2, …, 8) in their homogeneous coordinates is written as

Using the given scales along the x , y , z axes, the scaling matrix Eq. (2.6) is given as
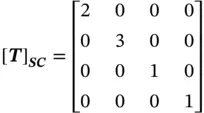
Therefore, the set of vertices of the object after scaling transformation can be found as
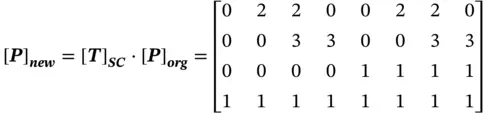
A 3D reflection refers to a transformation of mirroring an object about a specified plane. A reflection transformation matrix can be treated as a special case of a scaling matrix, where the scale of the corresponding axis of the reflected coordinate is set as a negative value of −1. Note that the axis for the reflection is aligned with the normal reflecting or mirroring plane. Therefore, the reflection coordination transformations about YZ, XZ, and XYplanes are expressed by [ T] RE_YZ, [ T] RE_XZ, and [ T] RE_XZ, respectively, as follows:
(2.7) 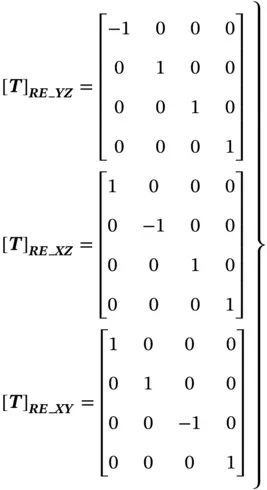
Figure 2.12a shows an object in the coordinate system ( O‐XYZ) with the specified set of vertices as follows:

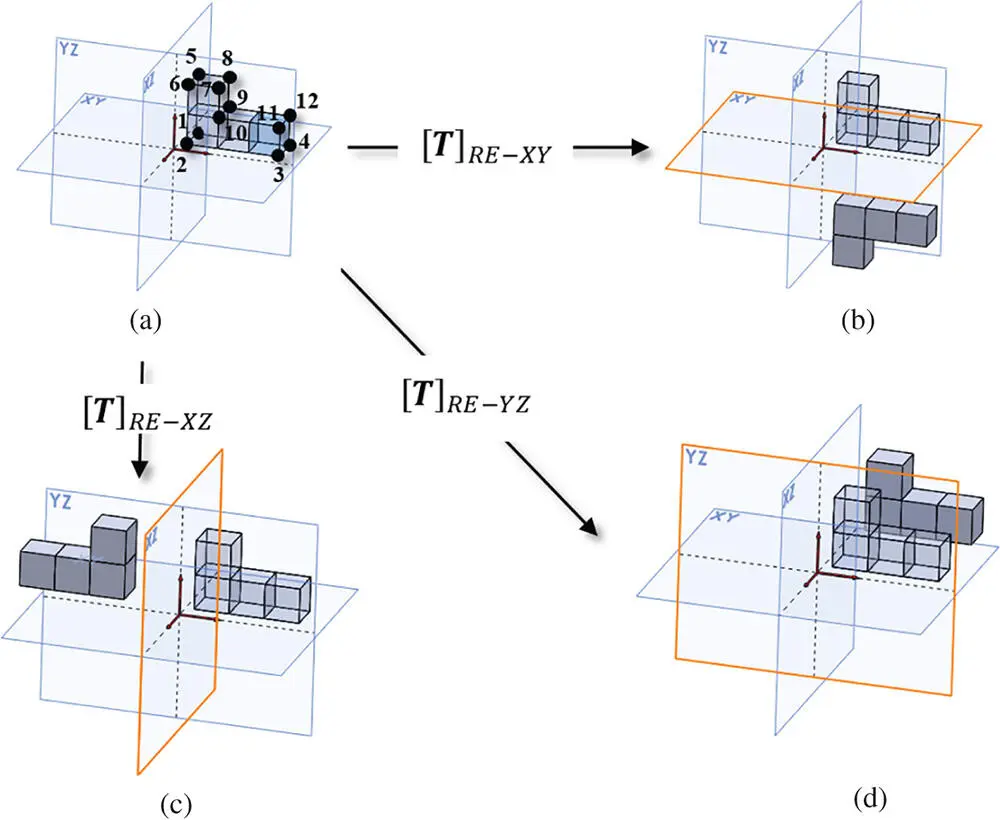
Figure 2.12Reflection coordinate transformation matrices of an object. (a) Object at the original position. (b) Reflected object about the XYplane. (c) Reflected object about the YZplane. (d) Reflected object about the YZplane.
Determine the reflected objects about the XY, YZ, XZplanes, respectively.
Using Eq. (2.7), the vertices of the reflected objects about the XY, YZ, XZplanes are determined and illustrated in Figure 2.12b to d, respectively. Taking as an example determination of the reflected object about the XY plane,
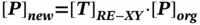
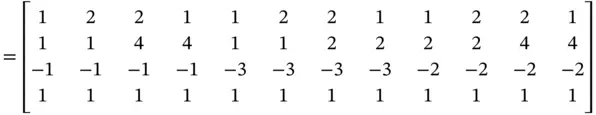
where [ T] RE − XYis given in Eq. (2.7) for the reflected object about the XYplane.
Читать дальше


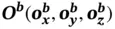 is used to represent the position of the object with respect to the world coordinate system ( O w− X w Y w Z w) and the orientation of the object is represented by three unit vectors ( X b, Y b, Z b). Furthermore, a homogeneous coordinate ( x , y , z , h ) and the corresponding 4 by 4 homogenous matrix [ T] 4x4in Eq. (2.4) are widely used to facilitate the matrix manipulations for the coordinate transformation of objects:
is used to represent the position of the object with respect to the world coordinate system ( O w− X w Y w Z w) and the orientation of the object is represented by three unit vectors ( X b, Y b, Z b). Furthermore, a homogeneous coordinate ( x , y , z , h ) and the corresponding 4 by 4 homogenous matrix [ T] 4x4in Eq. (2.4) are widely used to facilitate the matrix manipulations for the coordinate transformation of objects: