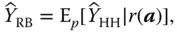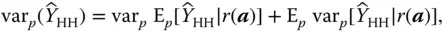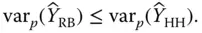A third solution consists of calculating the so‐called Rao–Blackwellized estimator. Without going into the technical details, it is possible to show that in the design‐based theory, the minimal sufficient statistic can be constructed by removing the information concerning the multiplicity of units. In other words, if a unit is selected several times in the sample with replacement, it is conserved only once (Basu & Ghosh, 1967; Basu, 1969; Cassel et al., 1977, 1993; Thompson & Seber, 1996, p. 35). Knowing a minimal sufficient statistic, one can then calculate the augmented estimator (also called the Rao–Blackwellized estimator) by conditioning an estimator with respect to the minimal sufficient statistic.
Concretely, we calculate the conditional expectation 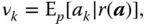 for all
for all 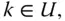 where
where 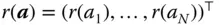 . Since
. Since 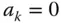 implies that
implies that 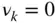 , we can define the Rao–Blackwellized estimator (RB):
, we can define the Rao–Blackwellized estimator (RB):
(2.9) 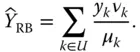
This estimator is unbiased because 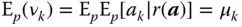 . Moreover, since
. Moreover, since
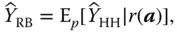
and
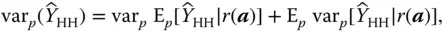
we have
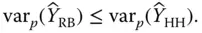
The Hansen–Hurwitz estimator should therefore in principle never be used. It is said that the Hansen–Hurwitz estimator is not admissible in the sense that it can always be improved by calculating its conditional expectation. However, this conditional expectation can sometimes be very complex to calculate. Rao–Blackwellization is at the heart of the theory of adaptive sampling, which can lead to multiple selections of the same unit in the sample (Thompson, 1990; Félix‐Medina, 2000; Thompson, 1991a; Thompson & Seber, 1996).
1 2.1 Show that
2 2.2 Let be a population with the following sampling design:Give the first‐order inclusion probabilities. Give the variance–covariance matrix of the indicator variables.
3 2.3 Let and have the following sampling design:Give the probability distributions of the expansion estimator and the Hájek estimator of the mean. Give the probability distributions of the two variance estimators of the expansion estimator and calculate their bias.Give the probability distributions of the two variance estimators of the expansion estimator of the mean in the case where .
4 2.4 Let be a sampling design without replacement applied to a population of size . Let and denote the first‐ and second‐order inclusion probabilities, respectively, and is the random sample. Consider the following estimator:For which function of interest is this estimator unbiased?
5 2.5 For a design without replacement with strictly positive inclusion probabilities, construct an unbiased estimator for .
6 2.6 Let be a finite population and let be the random sample of obtained by means of a design with inclusion probabilities and We suppose that this design is balanced on a variable . In other words,(2.10) The total of the variable of interest isand can be unbiasedly estimated byShow that(2.11) What particular result do we obtain when ?Show that (2.12)What result is generalized by Expression ( 2.12)?Construct an unbiased variance estimator from Expression ( 2.12).
7 2.7 Let be the variance–covariance matrix of the indicators of the presence of the units in the sample for a design :Is this design of fixed sample size?Does this design satisfy the Yates–Grundy conditions?Calculate the inclusion probabilities of this design knowing thatGive the matrix of the second‐order inclusion probabilities.Give the probabilities associated with all possible samples.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

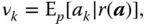 for all
for all 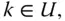 where
where 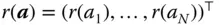 . Since
. Since 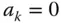 implies that
implies that 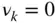 , we can define the Rao–Blackwellized estimator (RB):
, we can define the Rao–Blackwellized estimator (RB):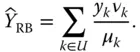
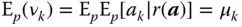 . Moreover, since
. Moreover, since