Yves Tille - Sampling and Estimation from Finite Populations

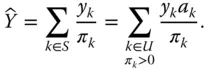
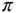This estimator was proposed by Narain (1951) and Horvitz & Thompson (1952). It is often called the Horvitz–Thompson estimator, but Narain's article precedes that of Horvitz–Thompson. It may also be referred to as the Narain or Narain–Horvitz–Thompson estimator or ‐estimator or estimator by dilated values.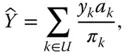

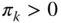Often, one writes

but this is correct only if , for all If any inclusion probabilities are zero, then 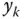is divided by 0. Of course, if an inclusion probability is zero, the corresponding unit is never selected in the sample.

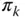In this estimator, the values taken by the variable are weighted by the inverse of their inclusion probabilities. The inverse of is often denoted by 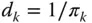and can be interpreted as the number of units that unit 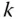represents in the population. The value 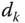is the weight assigned to unit 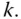The expansion estimator can also be written as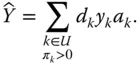

A necessary and sufficient condition for the expansion estimator to be unbiased is that 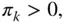for all .

Since

the bias of the estimator is

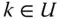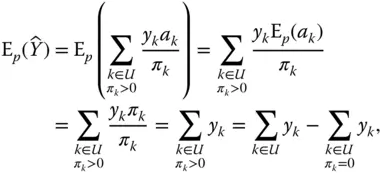
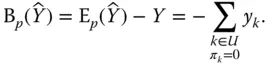
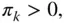The bias is zero if and only if for all

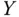If some inclusion probabilities are zero, it is impossible to estimate without bias. It is said that the sampling design does not cover the population or is vitiated by a coverage problem. We sometimes hear that a sample is biased, but this terminology should be avoided because bias is a property of an estimator and not of a sample. In what follows, we will consider that all the sampling designs have nonzero first‐order inclusion probabilities.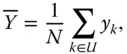

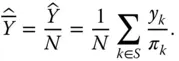
For estimating the mean

we can simply divide the expansion estimator of the total by the size of the population. We obtain

However, the population size is not necessarily known.

Estimator is unbiased, but it suffers from a serious problem. If the variable of interest 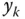is constant, in other words, 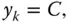then

(2.1)

Indeed, there is no reason that

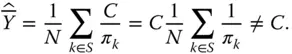
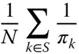
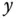is equal to 1, even if the expectation of this quantity is equal to 1. The expansion estimator of the mean is thus vitiated by an error that does not depend on the variability of variable . Even if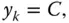 remains random.

We refer to the following definition:

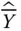An estimator of the mean is said to be linearly invariant if, for all 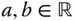, w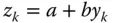hen then