Yves Tille - Sampling and Estimation from Finite Populations

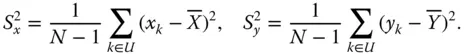
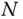The population size is not necessarily known and therefore can also be an estimation objective. However, as one can write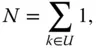

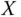the estimation of the population size is a problem of the same nature as the estimation of or .

Some parameters may depend jointly on two variables, such as the ratio of two totals,

the population covariance,

or the correlation coefficient,

These parameters are unknown and will therefore be estimated using a sample.

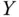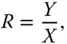
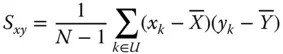
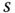A sample without replacement is simply a subset of the population 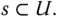We also consider the set 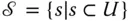of all the possible samples. For instance, if 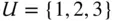, then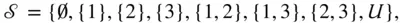

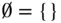where denotes the empty set.

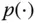A sampling design without replacement is a probability distribution on 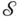such that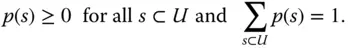

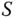A random sample is a random variable whose values are the samples: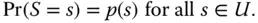

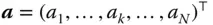A random sample can also be defined as a discrete random vector composed of non‐negative integer variables . The variable 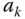represents the number of times unit 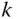is selected in the sample. If the sample is without replacement then variable 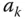can only take the values 0 or 1 and therefore has a Bernoulli distribution. In general, random variables 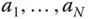are not independent except in very special cases. The use of indicator variables 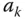was introduced by Cornfield (1944) and greatly simplified the notation in survey sampling theory because it allows us to clearly separate the values of the variables 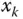or 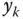from the source of randomness .

Often, we try to select the sample as randomly as possible. The usual measure of randomness of a probability distribution is the entropy.

The entropy of a sampling design is the quantity

We suppose that

We can search for sampling designs that maximize the entropy, with constraints such as a fixed sample size or given inclusion probabilities (see Section 2.3). A very random sampling design has better asymptotic properties and allows a more reliable inference (Berger, 1996, 1998a; Brewer & Donadio, 2003).

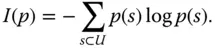
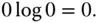
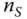The sample size is the number of units selected in the sample. We can write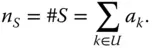

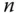When the sample size is not random, we say that the sample is of fixed sample size and we simply denote it by .